Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 101011 by Dwaipayan Shikari last updated on 29/Jun/20

∫_0 ^∞ ((sinx)/x)dx

$$\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}}{dx} \\ $$

Commented by Rohit@Thakur last updated on 29/Jun/20

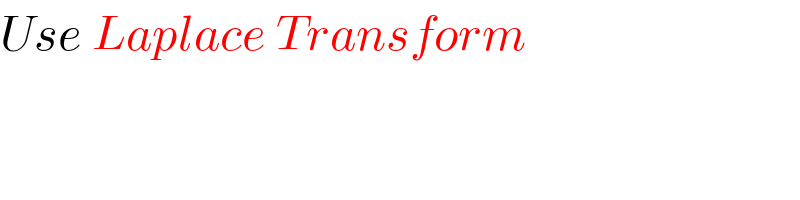
Use Laplace Transform

$${Use}\:{Laplace}\:{Transform} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by Rohit@Thakur last updated on 29/Jun/20

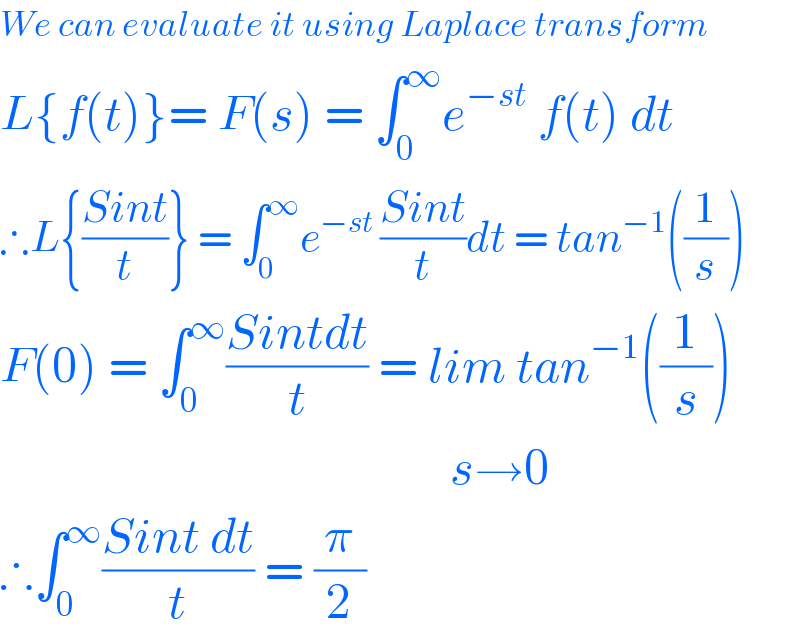
We can evaluate it using Laplace transform L{f(t)}= F(s) = ∫_0 ^∞ e^(−st) f(t) dt ∴L{((Sint)/t)} = ∫_0 ^∞ e^(−st ) ((Sint)/t)dt = tan^(−1) ((1/s)) F(0) = ∫_0 ^∞ ((Sintdt)/t) = lim tan^(−1) ((1/s)) s→0 ∴∫_0 ^∞ ((Sint dt)/t) = (π/2)

$${We}\:{can}\:{evaluate}\:{it}\:{using}\:{Laplace}\:{transform} \\ $$$${L}\left\{{f}\left({t}\right)\right\}=\:{F}\left({s}\right)\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} \:{f}\left({t}\right)\:{dt} \\ $$$$\therefore{L}\left\{\frac{{Sint}}{{t}}\right\}\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−{st}\:} \frac{{Sint}}{{t}}{dt}\:=\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}}\right) \\ $$$${F}\left(\mathrm{0}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{Sintdt}}{{t}}\:=\:{lim}\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{s}\rightarrow\mathrm{0} \\ $$$$\therefore\int_{\mathrm{0}} ^{\infty} \frac{{Sint}\:{dt}}{{t}}\:=\:\frac{\pi}{\mathrm{2}} \\ $$

Commented by Dwaipayan Shikari last updated on 29/Jun/20

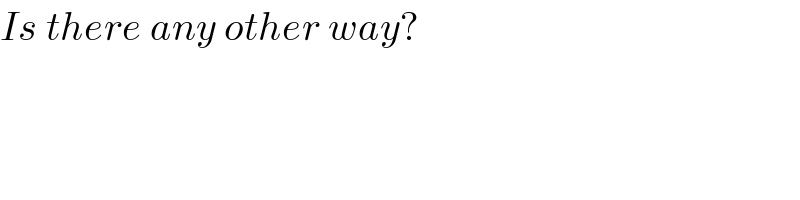
Is there any other way?

$${Is}\:{there}\:{any}\:{other}\:{way}? \\ $$

Commented by smridha last updated on 29/Jun/20

let′s do it by Feynman Technique let I(a)=∫_0 ^∞ ((sin(x))/x).e^(−ax) dx so I(0)=∫_0 ^∞ ((sin(x))/x) dx and I(∞)=0[aslim_(a→∞) e^(−ax) =0] now diff:both sides wrt a we get (d/da)[I(a)]=∫_0 ^∞ ((sin(x))/x).(∂/∂a)(e^(−ax) )dx I^′ (a)=−∫_0 ^∞ sin(x).e^(−ax) dx=−(1/(a^2 +1)) now integrating both sides wrt a ∫_0 ^∞ I^′ (a)da=−∫_0 ^∞ (da/(a^2 +1))=−[tan^(−1) (a)]_0 ^∞ =−(𝛑/2) I(∞)−I(0)=−(𝛑/2) 0−∫_0 ^∞ ((sin(x))/x)dx=−(𝛑/2) so ∫_0 ^∞ ((sin(x))/x)dx=(𝛑/2).

$$\boldsymbol{{let}}'{s}\:\boldsymbol{{do}}\:\boldsymbol{{it}}\:\boldsymbol{{by}}\:\boldsymbol{{Feynman}}\:\boldsymbol{{Technique}} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{I}}\left(\boldsymbol{{a}}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}.\boldsymbol{{e}}^{−\boldsymbol{{ax}}} \boldsymbol{{dx}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}\:\boldsymbol{{dx}}\:\boldsymbol{{and}}\:\boldsymbol{{I}}\left(\infty\right)=\mathrm{0}\left[\boldsymbol{{as}}\underset{\boldsymbol{{a}}\rightarrow\infty} {\mathrm{lim}}\boldsymbol{{e}}^{−\boldsymbol{{ax}}} =\mathrm{0}\right] \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{diff}}:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{wrt}}\:\boldsymbol{{a}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\frac{\boldsymbol{{d}}}{\boldsymbol{{da}}}\left[\boldsymbol{{I}}\left(\boldsymbol{{a}}\right)\right]=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}.\frac{\partial}{\partial\boldsymbol{{a}}}\left(\boldsymbol{{e}}^{−\boldsymbol{{ax}}} \right)\boldsymbol{{dx}} \\ $$$$\boldsymbol{{I}}^{'} \left(\boldsymbol{{a}}\right)=−\int_{\mathrm{0}} ^{\infty} \boldsymbol{{sin}}\left(\boldsymbol{{x}}\right).\boldsymbol{{e}}^{−\boldsymbol{{ax}}} \boldsymbol{{dx}}=−\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{integrating}}\:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{wrt}}\:\boldsymbol{{a}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \boldsymbol{{I}}^{'} \left(\boldsymbol{{a}}\right)\boldsymbol{{da}}=−\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{da}}}{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{1}}=−\left[\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{a}}\right)\right]_{\mathrm{0}} ^{\infty} =−\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\boldsymbol{{I}}\left(\infty\right)−\boldsymbol{{I}}\left(\mathrm{0}\right)=−\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\mathrm{0}−\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}}=−\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\boldsymbol{{so}}\:\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}}=\frac{\boldsymbol{\pi}}{\mathrm{2}}. \\ $$$$ \\ $$

Commented by smridha last updated on 29/Jun/20

another way I=∫_0 ^∞ ((sinx)/x)dx by Cauchy principal value theorem we get I=p∫_(−∞) ^(+∞) (e^(ix) /(2ix))dx now two semi−infinite segments costituting the pricipal value integral (i)semicircle C_R of redius(R⇒∞) (ii)semicircle C_r of redius (r⇒0) is taken clockwise now ∮(e^(iz) /(2iz))dz=I+∫_c_r (e^(iz) /(2iz))dz+∫_c_R (e^(iz) /(2iz))dz=0 by Jordan′s lemma the integral over C_R vanishes. the clockwise path C_r half way around the pole z=0 contributes half the value of full circuit so the residue around the pole z=0 is (1/(2i)) so ∫_c_r =−𝛑i.(1/(2i))=−(𝛑/2) so I=(𝛑/2).

$$\boldsymbol{{another}}\:\boldsymbol{{way}} \\ $$$$\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}\boldsymbol{{dx}} \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{Cauchy}}\:\boldsymbol{{principal}}\:\boldsymbol{{value}}\:\boldsymbol{{theorem}} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\boldsymbol{{I}}=\boldsymbol{{p}}\int_{−\infty} ^{+\infty} \frac{\boldsymbol{{e}}^{\boldsymbol{{ix}}} }{\mathrm{2}\boldsymbol{{ix}}}\boldsymbol{{dx}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{two}}\:\boldsymbol{{semi}}−\boldsymbol{{infinite}}\:\boldsymbol{{segments}} \\ $$$$\boldsymbol{{costituting}}\:\boldsymbol{{the}}\:\boldsymbol{{pricipal}}\:\boldsymbol{{value}}\:\boldsymbol{{integral}} \\ $$$$\left(\boldsymbol{{i}}\right)\boldsymbol{{semicircle}}\:\boldsymbol{{C}}_{\boldsymbol{{R}}} \boldsymbol{{of}}\:\boldsymbol{{redius}}\left(\boldsymbol{{R}}\Rightarrow\infty\right) \\ $$$$\left(\boldsymbol{{ii}}\right)\boldsymbol{{semicircle}}\:\boldsymbol{{C}}_{\boldsymbol{{r}}} \:\boldsymbol{{of}}\:\boldsymbol{{redius}}\:\left(\boldsymbol{{r}}\Rightarrow\mathrm{0}\right) \\ $$$$\:\boldsymbol{{is}}\:\boldsymbol{{taken}}\:\boldsymbol{{clockwise}}\:\boldsymbol{{now}} \\ $$$$\oint\frac{\boldsymbol{{e}}^{\boldsymbol{{iz}}} }{\mathrm{2}\boldsymbol{{iz}}}\boldsymbol{{dz}}=\boldsymbol{{I}}+\int_{\boldsymbol{{c}}_{\boldsymbol{{r}}} } \frac{\boldsymbol{{e}}^{\boldsymbol{{iz}}} }{\mathrm{2}\boldsymbol{{iz}}}\boldsymbol{{dz}}+\int_{\boldsymbol{{c}}_{\boldsymbol{{R}}} } \frac{\boldsymbol{{e}}^{\boldsymbol{{iz}}} }{\mathrm{2}\boldsymbol{{iz}}}\boldsymbol{{dz}}=\mathrm{0} \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{J}}{o}\boldsymbol{{rdan}}'{s}\:\boldsymbol{{lemma}}\:\boldsymbol{{the}}\:\boldsymbol{{integral}} \\ $$$$\boldsymbol{{over}}\:\boldsymbol{{C}}_{{R}} \:\boldsymbol{{vanishes}}. \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{clockwise}}\:\boldsymbol{{path}}\:\boldsymbol{{C}}_{\boldsymbol{{r}}} \:\boldsymbol{{half}}\:\boldsymbol{{way}} \\ $$$$\boldsymbol{{around}}\:\boldsymbol{{the}}\:\boldsymbol{{pole}}\:\boldsymbol{{z}}=\mathrm{0}\:\boldsymbol{{contributes}} \\ $$$$\boldsymbol{{half}}\:\boldsymbol{{the}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{full}}\:\boldsymbol{{circuit}} \\ $$$$\boldsymbol{{so}}\:\:\boldsymbol{{the}}\:\boldsymbol{{residue}}\:\boldsymbol{{around}}\:\boldsymbol{{the}}\:\boldsymbol{{pole}} \\ $$$$\boldsymbol{{z}}=\mathrm{0}\:\boldsymbol{{is}}\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{i}}}\:\boldsymbol{{so}}\:\int_{\boldsymbol{{c}}_{\boldsymbol{{r}}} } =−\boldsymbol{\pi{i}}.\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{i}}}=−\frac{\boldsymbol{\pi}}{\mathrm{2}}\: \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}=\frac{\boldsymbol{\pi}}{\mathrm{2}}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com