Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 152141 by Ar Brandon last updated on 26/Aug/21

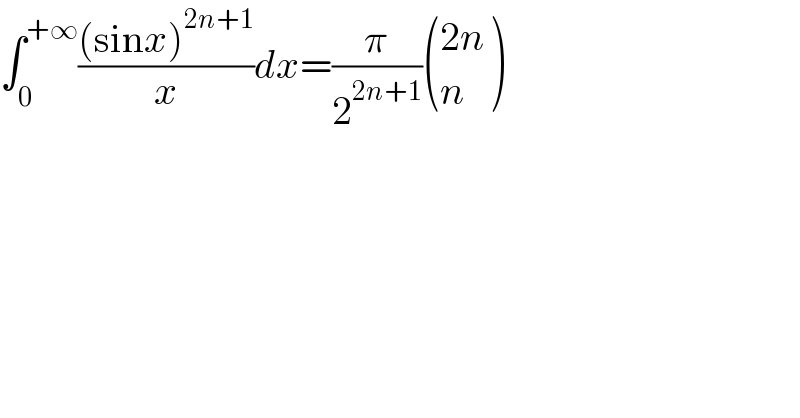
∫_0 ^(+∞) (((sinx)^(2n+1) )/x)dx=(π/2^(2n+1) ) (((2n)),(n) )

$$\int_{\mathrm{0}} ^{+\infty} \frac{\left(\mathrm{sin}{x}\right)^{\mathrm{2}{n}+\mathrm{1}} }{{x}}{dx}=\frac{\pi}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix} \\ $$

Answered by Olaf_Thorendsen last updated on 26/Aug/21

I_n = ∫_0 ^(+∞) ((sin^(2n+1) x)/x) dx Let f(x) = sin^(2n) x I_n = ∫_0 ^(+∞) ((sinx)/x)f(x) dx f is a π−periodic function. We can apply the Lobachevsky−Dirchlet integral formula : ∫_0 ^(+∞) ((sinx)/x)f(x) dx = ∫_0 ^(π/2) f(x)dx ⇒ I_n = ∫_0 ^(π/2) sin^(2n) x dx = W_(2n) = (π/2).(((2n)!)/((2^n n!)^2 )) (W_(2n) : integral of Wallis) I_n = (π/2^(2n+1) ).(((2n)!)/(n!n!)) = (π/2^(2n+1) )C_n ^(2n)

$$\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{sin}^{\mathrm{2}{n}+\mathrm{1}} {x}}{{x}}\:{dx} \\ $$$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\mathrm{sin}^{\mathrm{2}{n}} {x} \\ $$$$\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{sin}{x}}{{x}}{f}\left({x}\right)\:{dx} \\ $$$$ \\ $$$${f}\:\mathrm{is}\:\mathrm{a}\:\pi−\mathrm{periodic}\:\mathrm{function}.\:\mathrm{We}\:\mathrm{can} \\ $$$$\mathrm{apply}\:\mathrm{the}\:\mathrm{Lobachevsky}−\mathrm{Dirchlet} \\ $$$$\mathrm{integral}\:\mathrm{formula}\:: \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{sin}{x}}{{x}}{f}\left({x}\right)\:{dx}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({x}\right){dx} \\ $$$$\Rightarrow\:\mathrm{I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}{n}} {x}\:{dx}\:=\:{W}_{\mathrm{2}{n}} \:=\:\frac{\pi}{\mathrm{2}}.\frac{\left(\mathrm{2}{n}\right)!}{\left(\mathrm{2}^{{n}} {n}!\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{W}_{\mathrm{2}{n}} \::\:\mathrm{integral}\:\mathrm{of}\:\mathrm{Wallis}\right) \\ $$$$\mathrm{I}_{{n}} \:=\:\frac{\pi}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }.\frac{\left(\mathrm{2}{n}\right)!}{{n}!{n}!}\:=\:\frac{\pi}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\mathrm{C}_{{n}} ^{\mathrm{2}{n}} \\ $$

Commented by Ar Brandon last updated on 26/Aug/21

Grac_ξ ias sen^ or !

$$\mathrm{Gra} ext{\c{c}} \mathrm{cias}\:\mathrm{se}\overset{ } {\mathrm{n}or}\:! \\ $$

Commented by puissant last updated on 26/Aug/21

hum

$${hum} \\ $$

Answered by Kamel last updated on 26/Aug/21

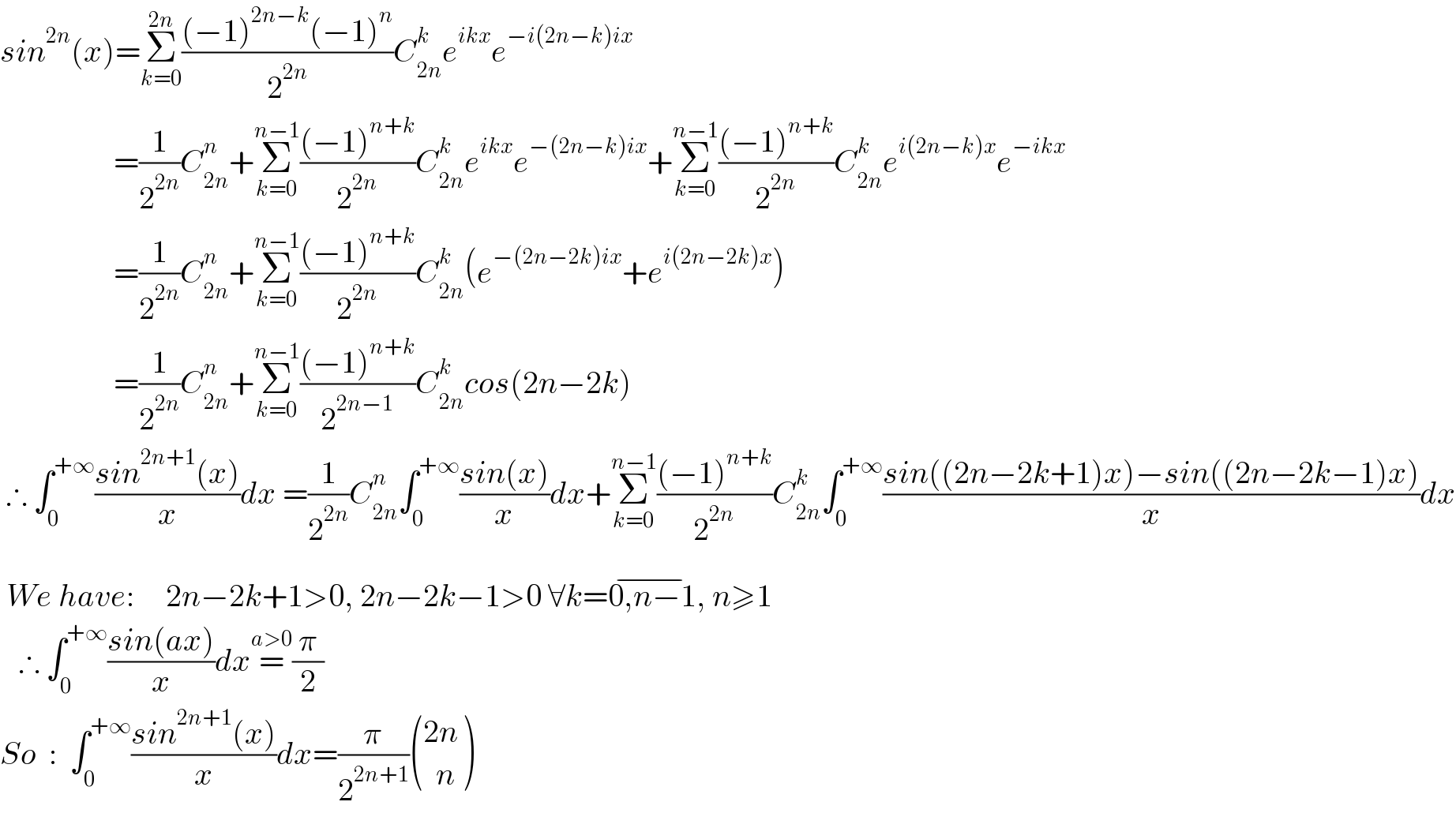
sin^(2n) (x)=Σ_(k=0) ^(2n) (((−1)^(2n−k) (−1)^n )/2^(2n) )C_(2n) ^k e^(ikx) e^(−i(2n−k)ix) =(1/2^(2n) )C_(2n) ^n +Σ_(k=0) ^(n−1) (((−1)^(n+k) )/2^(2n) )C_(2n) ^k e^(ikx) e^(−(2n−k)ix) +Σ_(k=0) ^(n−1) (((−1)^(n+k) )/2^(2n) )C_(2n) ^k e^(i(2n−k)x) e^(−ikx) =(1/2^(2n) )C_(2n) ^n +Σ_(k=0) ^(n−1) (((−1)^(n+k) )/2^(2n) )C_(2n) ^k (e^(−(2n−2k)ix) +e^(i(2n−2k)x) ) =(1/2^(2n) )C_(2n) ^n +Σ_(k=0) ^(n−1) (((−1)^(n+k) )/2^(2n−1) )C_(2n) ^k cos(2n−2k) ∴ ∫_0 ^(+∞) ((sin^(2n+1) (x))/x)dx =(1/2^(2n) )C_(2n) ^n ∫_0 ^(+∞) ((sin(x))/x)dx+Σ_(k=0) ^(n−1) (((−1)^(n+k) )/2^(2n) )C_(2n) ^k ∫_0 ^(+∞) ((sin((2n−2k+1)x)−sin((2n−2k−1)x))/x)dx We have: 2n−2k+1>0, 2n−2k−1>0 ∀k=0,n−1^(−) , n≥1 ∴ ∫_0 ^(+∞) ((sin(ax))/x)dx=^(a>0) (π/2) So : ∫_0 ^(+∞) ((sin^(2n+1) (x))/x)dx=(π/2^(2n+1) ) (((2n)),(( n)) )

$${sin}^{\mathrm{2}{n}} \left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{2}{n}−{k}} \left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{k}} {e}^{{ikx}} {e}^{−{i}\left(\mathrm{2}{n}−{k}\right){ix}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{n}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+{k}} }{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{k}} {e}^{{ikx}} {e}^{−\left(\mathrm{2}{n}−{k}\right){ix}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+{k}} }{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{k}} {e}^{{i}\left(\mathrm{2}{n}−{k}\right){x}} {e}^{−{ikx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{n}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+{k}} }{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{k}} \left({e}^{−\left(\mathrm{2}{n}−\mathrm{2}{k}\right){ix}} +{e}^{{i}\left(\mathrm{2}{n}−\mathrm{2}{k}\right){x}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{n}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+{k}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }{C}_{\mathrm{2}{n}} ^{{k}} {cos}\left(\mathrm{2}{n}−\mathrm{2}{k}\right) \\ $$$$\:\therefore\:\int_{\mathrm{0}} ^{+\infty} \frac{{sin}^{\mathrm{2}{n}+\mathrm{1}} \left({x}\right)}{{x}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{n}} \int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left({x}\right)}{{x}}{dx}+\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+{k}} }{\mathrm{2}^{\mathrm{2}{n}} }{C}_{\mathrm{2}{n}} ^{{k}} \int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left(\left(\mathrm{2}{n}−\mathrm{2}{k}+\mathrm{1}\right){x}\right)−{sin}\left(\left(\mathrm{2}{n}−\mathrm{2}{k}−\mathrm{1}\right){x}\right)}{{x}}{dx} \\ $$$$\:{We}\:{have}:\:\:\:\:\:\mathrm{2}{n}−\mathrm{2}{k}+\mathrm{1}>\mathrm{0},\:\mathrm{2}{n}−\mathrm{2}{k}−\mathrm{1}>\mathrm{0}\:\forall{k}=\overline {\mathrm{0},{n}−\mathrm{1}},\:{n}\geqslant\mathrm{1} \\ $$$$\:\:\:\therefore\:\int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left({ax}\right)}{{x}}{dx}\overset{{a}>\mathrm{0}} {=}\frac{\pi}{\mathrm{2}} \\ $$$${So}\:\::\:\:\int_{\mathrm{0}} ^{+\infty} \frac{{sin}^{\mathrm{2}{n}+\mathrm{1}} \left({x}\right)}{{x}}{dx}=\frac{\pi}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\begin{pmatrix}{\mathrm{2}{n}}\\{\:\:{n}}\end{pmatrix} \\ $$

Commented by Ar Brandon last updated on 26/Aug/21

Oh my! Thanks Sir

$$\mathrm{Oh}\:\mathrm{my}!\:\mathrm{Thanks}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com