
Question Number 151449 by mathdanisur last updated on 21/Aug/21
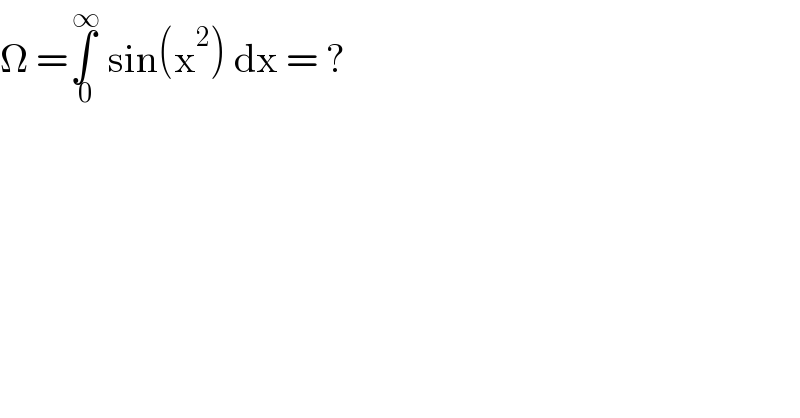
$$\Omega\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)\:\mathrm{dx}\:=\:? \\ $$
Answered by puissant last updated on 21/Aug/21
![f(u)=e^(−u^2 ) ⇒ ∮f(u)du=∫_0 ^a e^(−t^2 ) dt+∫_0 ^(π/4) iae^(it) e^(−a^2 exp(2it)) dt−∫_0 ^a e^(i(π/4)) e^(−it^2 ) dt I_1 =∫_0 ^a e^(−t^2 ) dt I_2 =∫_0 ^(π/4) iae^(it) e^(−a^2 exp(2it)) dt I_3 =∫_0 ^a e^(i(π/4)) e^(−it^2 ) dt ∣I_2 (a)∣≤∫_0 ^(π/4) ae^(−a^2 cos(2t)) dt=∫_0 ^(π/2) (a/2)e^(−a^2 cosz) dz ∀u∈[0;(π/2)], 1−((2z)/π)≤cosz≤1 ⇒ ∀u∈[0;(π/2)], e^(−a^2 cosz) ≤e^(a^2 (((2z)/π)−1)) ⇒ ∫_0 ^(π/2) (a/2)e^(−a^2 cosz) dz≤(π/(4a))(1−e^(−a^2 ) ) lim_(a→∞) I_2 (a)=0 (gendarme theoreme) I_1 (a)=((√π)/2) (Gauss integrale) lim_(a→∞) I_3 (a)=∫_0 ^∞ e^(i(π/4)) e^(−it^2 ) dt = ((1+i)/( (√2)))∫_0 ^∞ e^(−it^2 ) dt f parcout une distance ferme, ⇒ ∮f(u)du=0 ⇒ ((1+i)/( (√2)))∫_0 ^∞ e^(−it^2 ) dt=((√π)/2) ⇒ ∫_0 ^∞ e^(−it^2 ) dt=(((1−i)/2))(√(π/2)) Q=∫_0 ^∞ sin(x^2 )dx=Im(∫_0 ^∞ e^(−it^2 ) dt)=(√(π/8))..■ Remarque: ∫_0 ^∞ sin(x^2 )dx=∫_0 ^∞ cos(x^2 )dx=(√(π/8))..★ appele Integrale de FRESNEL.. ..............Le puissant..............](Q151455.png)
$${f}\left({u}\right)={e}^{−{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\oint{f}\left({u}\right){du}=\int_{\mathrm{0}} ^{{a}} {e}^{−{t}^{\mathrm{2}} } {dt}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {iae}^{{it}} {e}^{−{a}^{\mathrm{2}} {exp}\left(\mathrm{2}{it}\right)} {dt}−\int_{\mathrm{0}} ^{{a}} {e}^{{i}\frac{\pi}{\mathrm{4}}} {e}^{−{it}^{\mathrm{2}} } {dt} \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{{a}} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {iae}^{{it}} {e}^{−{a}^{\mathrm{2}} {exp}\left(\mathrm{2}{it}\right)} {dt} \\ $$$${I}_{\mathrm{3}} =\int_{\mathrm{0}} ^{{a}} {e}^{{i}\frac{\pi}{\mathrm{4}}} {e}^{−{it}^{\mathrm{2}} } {dt} \\ $$$$\mid{I}_{\mathrm{2}} \left({a}\right)\mid\leqslant\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ae}^{−{a}^{\mathrm{2}} {cos}\left(\mathrm{2}{t}\right)} {dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{a}}{\mathrm{2}}{e}^{−{a}^{\mathrm{2}} {cosz}} {dz} \\ $$$$\forall{u}\in\left[\mathrm{0};\frac{\pi}{\mathrm{2}}\right],\:\mathrm{1}−\frac{\mathrm{2}{z}}{\pi}\leqslant{cosz}\leqslant\mathrm{1} \\ $$$$\Rightarrow\:\forall{u}\in\left[\mathrm{0};\frac{\pi}{\mathrm{2}}\right],\:{e}^{−{a}^{\mathrm{2}} {cosz}} \leqslant{e}^{{a}^{\mathrm{2}} \left(\frac{\mathrm{2}{z}}{\pi}−\mathrm{1}\right)} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{a}}{\mathrm{2}}{e}^{−{a}^{\mathrm{2}} {cosz}} {dz}\leqslant\frac{\pi}{\mathrm{4}{a}}\left(\mathrm{1}−{e}^{−{a}^{\mathrm{2}} } \right) \\ $$$${lim}_{{a}\rightarrow\infty} {I}_{\mathrm{2}} \left({a}\right)=\mathrm{0}\:\left({gendarme}\:{theoreme}\right) \\ $$$${I}_{\mathrm{1}} \left({a}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}\:\left({Gauss}\:{integrale}\right) \\ $$$${lim}_{{a}\rightarrow\infty} {I}_{\mathrm{3}} \left({a}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{{i}\frac{\pi}{\mathrm{4}}} {e}^{−{it}^{\mathrm{2}} } {dt}\:=\:\frac{\mathrm{1}+{i}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} {e}^{−{it}^{\mathrm{2}} } {dt} \\ $$$${f}\:{parcout}\:{une}\:{distance}\:{ferme}, \\ $$$$\Rightarrow\:\oint{f}\left({u}\right){du}=\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}+{i}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} {e}^{−{it}^{\mathrm{2}} } {dt}=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\infty} {e}^{−{it}^{\mathrm{2}} } {dt}=\left(\frac{\mathrm{1}−{i}}{\mathrm{2}}\right)\sqrt{\frac{\pi}{\mathrm{2}}} \\ $$$${Q}=\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{\mathrm{2}} \right){dx}={Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−{it}^{\mathrm{2}} } {dt}\right)=\sqrt{\frac{\pi}{\mathrm{8}}}..\blacksquare \\ $$$${Remarque}:\:\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{\mathrm{2}} \right){dx}=\int_{\mathrm{0}} ^{\infty} {cos}\left({x}^{\mathrm{2}} \right){dx}=\sqrt{\frac{\pi}{\mathrm{8}}}..\bigstar \\ $$$${appele}\:{Integrale}\:{de}\:{FRESNEL}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:..............\mathscr{L}{e}\:{puissant}.............. \\ $$
Commented by mathdanisur last updated on 21/Aug/21
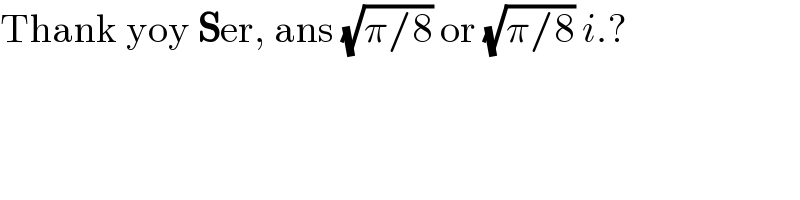
$$\mathrm{Thank}\:\mathrm{yoy}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{ans}\:\sqrt{\pi/\mathrm{8}}\:\mathrm{or}\:\sqrt{\pi/\mathrm{8}}\:{i}.? \\ $$
Commented by puissant last updated on 21/Aug/21
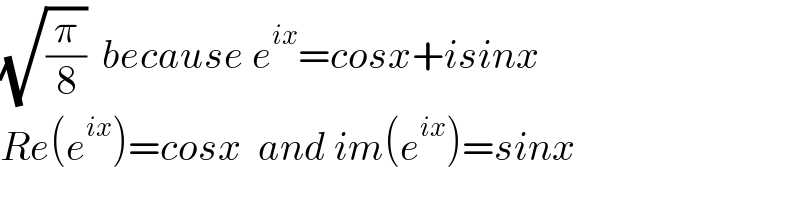
$$\sqrt{\frac{\pi}{\mathrm{8}}}\:\:{because}\:{e}^{{ix}} ={cosx}+{isinx} \\ $$$${Re}\left({e}^{{ix}} \right)={cosx}\:\:{and}\:{im}\left({e}^{{ix}} \right)={sinx} \\ $$
Answered by Ar Brandon last updated on 26/Aug/21
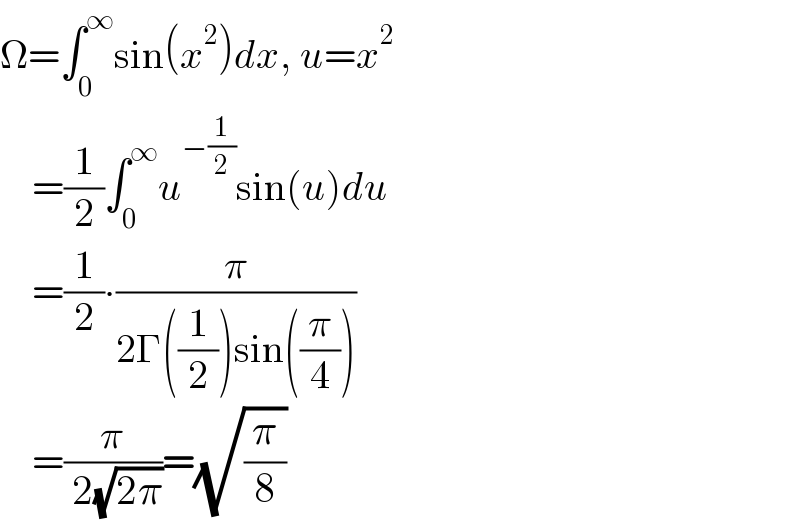
$$\Omega=\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\left({x}^{\mathrm{2}} \right){dx},\:{u}={x}^{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{sin}\left({u}\right){du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\pi}{\mathrm{2}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)} \\ $$$$\:\:\:\:=\frac{\pi}{\:\mathrm{2}\sqrt{\mathrm{2}\pi}}=\sqrt{\frac{\pi}{\mathrm{8}}} \\ $$
