
Question Number 5321 by qw last updated on 07/May/16
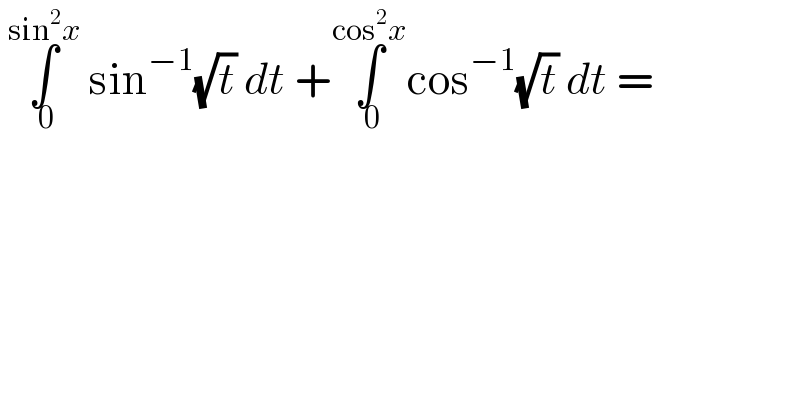
$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{sin}^{\mathrm{2}} {x}} {\int}}\:\mathrm{sin}^{−\mathrm{1}} \sqrt{{t}}\:{dt}\:+\underset{\:\mathrm{0}} {\overset{\mathrm{cos}^{\mathrm{2}} {x}} {\int}}\mathrm{cos}^{−\mathrm{1}} \sqrt{{t}}\:{dt}\:= \\ $$
Commented by Yozzii last updated on 08/May/16
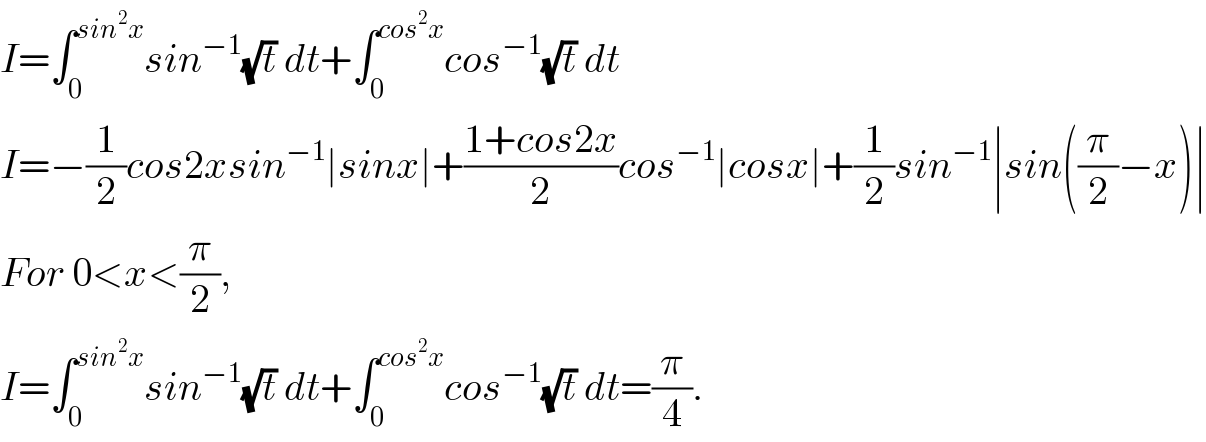
$${I}=\int_{\mathrm{0}} ^{{sin}^{\mathrm{2}} {x}} {sin}^{−\mathrm{1}} \sqrt{{t}}\:{dt}+\int_{\mathrm{0}} ^{{cos}^{\mathrm{2}} {x}} {cos}^{−\mathrm{1}} \sqrt{{t}}\:{dt} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{xsin}^{−\mathrm{1}} \mid{sinx}\mid+\frac{\mathrm{1}+{cos}\mathrm{2}{x}}{\mathrm{2}}{cos}^{−\mathrm{1}} \mid{cosx}\mid+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \mid{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\mid \\ $$$${For}\:\mathrm{0}<{x}<\frac{\pi}{\mathrm{2}}, \\ $$$${I}=\int_{\mathrm{0}} ^{{sin}^{\mathrm{2}} {x}} {sin}^{−\mathrm{1}} \sqrt{{t}}\:{dt}+\int_{\mathrm{0}} ^{{cos}^{\mathrm{2}} {x}} {cos}^{−\mathrm{1}} \sqrt{{t}}\:{dt}=\frac{\pi}{\mathrm{4}}. \\ $$
