Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 182771 by liuxinnan last updated on 14/Dec/22

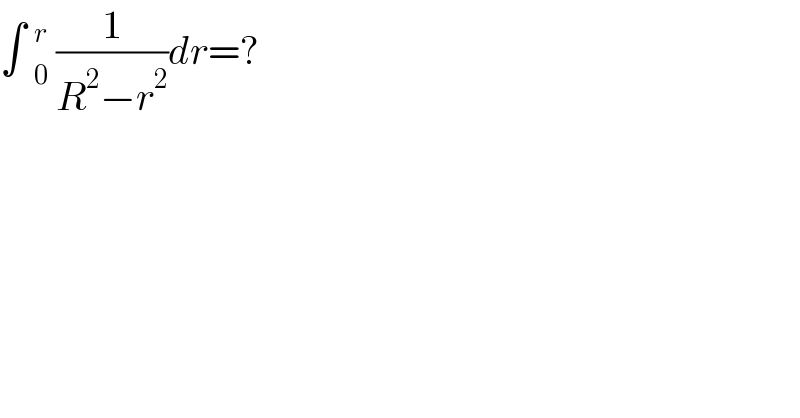
∫ _0^r (1/(R^2 −r^2 ))dr=?

$$\int\:_{\mathrm{0}} ^{{r}} \:\frac{\mathrm{1}}{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{dr}=? \\ $$

Commented by Frix last updated on 14/Dec/22

Error: dependent borders are not allowed.

$$\mathrm{Error}:\:\mathrm{dependent}\:\mathrm{borders}\:\mathrm{are}\:\mathrm{not}\:\mathrm{allowed}. \\ $$

Commented by mr W last updated on 14/Dec/22

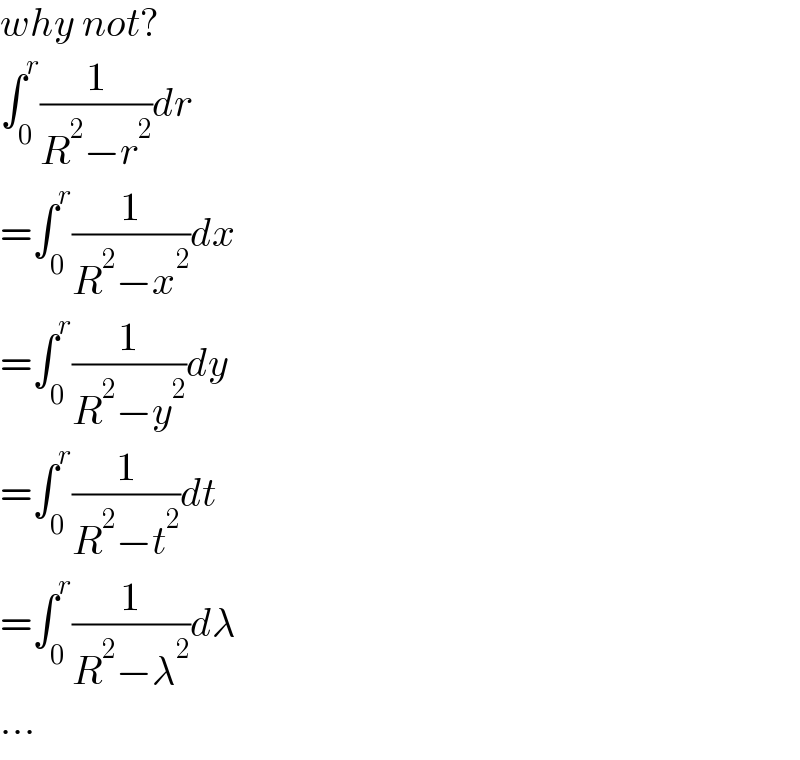
why not? ∫_0 ^r (1/(R^2 −r^2 ))dr =∫_0 ^r (1/(R^2 −x^2 ))dx =∫_0 ^r (1/(R^2 −y^2 ))dy =∫_0 ^r (1/(R^2 −t^2 ))dt =∫_0 ^r (1/(R^2 −λ^2 ))dλ ...

$${why}\:{not}? \\ $$$$\int_{\mathrm{0}} ^{{r}} \frac{\mathrm{1}}{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{dr} \\ $$$$=\int_{\mathrm{0}} ^{{r}} \frac{\mathrm{1}}{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{{r}} \frac{\mathrm{1}}{{R}^{\mathrm{2}} −{y}^{\mathrm{2}} }{dy} \\ $$$$=\int_{\mathrm{0}} ^{{r}} \frac{\mathrm{1}}{{R}^{\mathrm{2}} −{t}^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{{r}} \frac{\mathrm{1}}{{R}^{\mathrm{2}} −\lambda^{\mathrm{2}} }{d}\lambda \\ $$$$... \\ $$

Commented by Frix last updated on 14/Dec/22

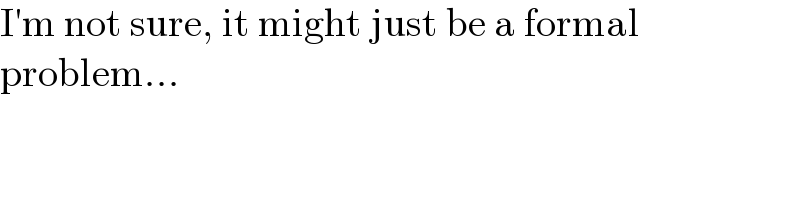
I′m not sure, it might just be a formal problem...

$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure},\:\mathrm{it}\:\mathrm{might}\:\mathrm{just}\:\mathrm{be}\:\mathrm{a}\:\mathrm{formal} \\ $$$$\mathrm{problem}... \\ $$

Commented by Frix last updated on 14/Dec/22

My thoughts: ∫f(x)dx=F(x)+C gives the antiderivative ∫_a ^b f(x)dx=F(b)−F(a) gives the area between f(x) and the x−axis ∫_a ^x f(x)dx=F(x)−F(a) gives what? I never needed this... anyway it′s the first case with C=−F(a)

$$\mathrm{My}\:\mathrm{thoughts}: \\ $$$$\int{f}\left({x}\right){dx}={F}\left({x}\right)+{C} \\ $$$$\:\:\:\:\:\mathrm{gives}\:\mathrm{the}\:\mathrm{antiderivative} \\ $$$$\underset{{a}} {\overset{{b}} {\int}}{f}\left({x}\right){dx}={F}\left({b}\right)−{F}\left({a}\right) \\ $$$$\:\:\:\:\:\mathrm{gives}\:\mathrm{the}\:\mathrm{area}\:\mathrm{between}\:{f}\left({x}\right)\:\mathrm{and}\:\mathrm{the}\:{x}−\mathrm{axis} \\ $$$$\underset{{a}} {\overset{{x}} {\int}}{f}\left({x}\right){dx}={F}\left({x}\right)−{F}\left({a}\right) \\ $$$$\:\:\:\:\:\mathrm{gives}\:{what}?\:\mathrm{I}\:\mathrm{never}\:\mathrm{needed}\:\mathrm{this}...\:\mathrm{anyway} \\ $$$$\:\:\:\:\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{first}\:\mathrm{case}\:\mathrm{with}\:{C}=−{F}\left({a}\right) \\ $$

Commented by mr W last updated on 14/Dec/22

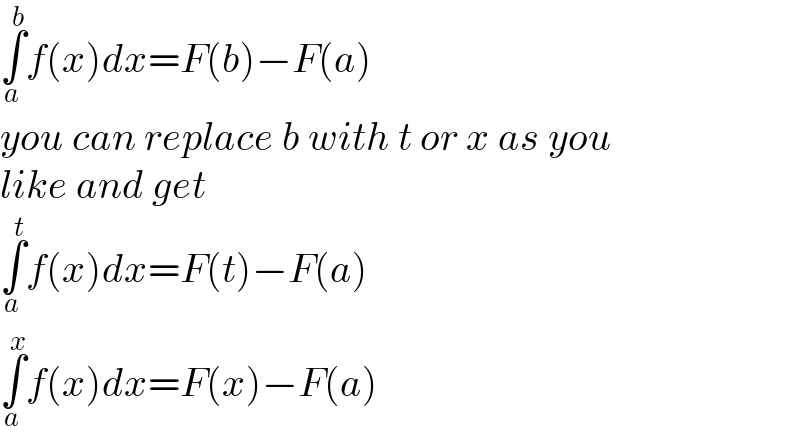
∫_a ^b f(x)dx=F(b)−F(a) you can replace b with t or x as you like and get ∫_a ^t f(x)dx=F(t)−F(a) ∫_a ^x f(x)dx=F(x)−F(a)

$$\underset{{a}} {\overset{{b}} {\int}}{f}\left({x}\right){dx}={F}\left({b}\right)−{F}\left({a}\right) \\ $$$${you}\:{can}\:{replace}\:{b}\:{with}\:{t}\:{or}\:{x}\:{as}\:{you} \\ $$$${like}\:{and}\:{get} \\ $$$$\underset{{a}} {\overset{{t}} {\int}}{f}\left({x}\right){dx}={F}\left({t}\right)−{F}\left({a}\right) \\ $$$$\underset{{a}} {\overset{{x}} {\int}}{f}\left({x}\right){dx}={F}\left({x}\right)−{F}\left({a}\right) \\ $$

Commented by mr W last updated on 14/Dec/22

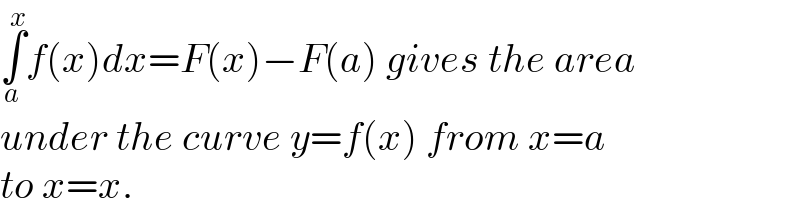
∫_a ^x f(x)dx=F(x)−F(a) gives the area under the curve y=f(x) from x=a to x=x.

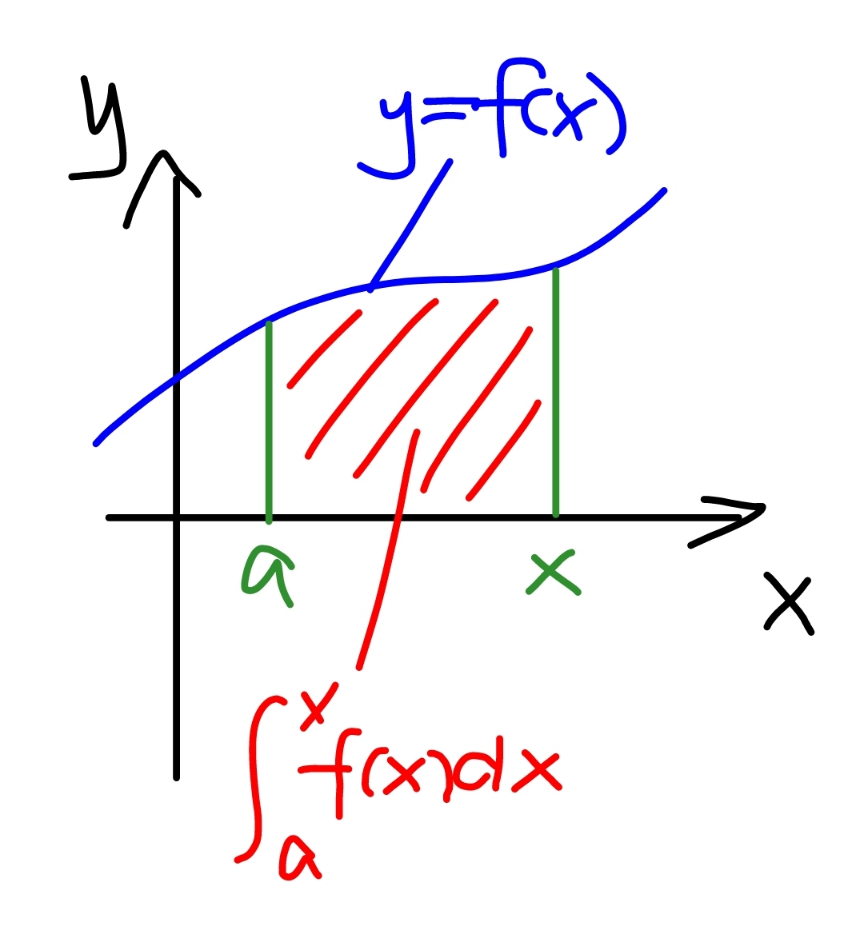
$$\underset{{a}} {\overset{{x}} {\int}}{f}\left({x}\right){dx}={F}\left({x}\right)−{F}\left({a}\right)\:{gives}\:{the}\:{area} \\ $$$${under}\:{the}\:{curve}\:{y}={f}\left({x}\right)\:{from}\:{x}={a}\: \\ $$$${to}\:{x}={x}. \\ $$

Commented by mr W last updated on 14/Dec/22

Answered by mr W last updated on 14/Dec/22

∫_0 ^r (1/(R^2 −r^2 ))dr =(1/(2R))∫_0 ^r ((1/(R−r))+(1/(R+r)))dr =(1/(2R)) [ln ((R+r)/(R−r))]_0 ^r =(1/(2R)) ln ((R+r)/(R−r))

$$\int_{\mathrm{0}} ^{{r}} \frac{\mathrm{1}}{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{R}}\int_{\mathrm{0}} ^{{r}} \left(\frac{\mathrm{1}}{{R}−{r}}+\frac{\mathrm{1}}{{R}+{r}}\right){dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{R}}\:\left[\mathrm{ln}\:\frac{{R}+{r}}{{R}−{r}}\right]_{\mathrm{0}} ^{{r}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{R}}\:\mathrm{ln}\:\frac{{R}+{r}}{{R}−{r}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com