
Question Number 151429 by peter frank last updated on 21/Aug/21
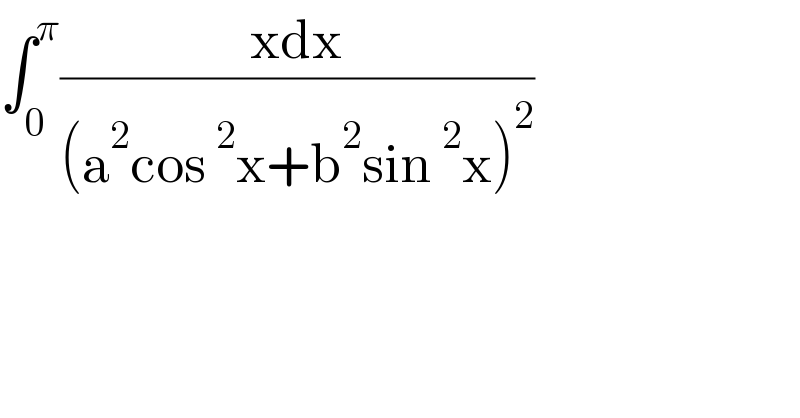
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{xdx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} } \\ $$
Answered by Olaf_Thorendsen last updated on 21/Aug/21
![I = ∫_0 ^π (x/((a^2 cos^2 x+b^2 sin^2 x)^2 )) dx Let u = π−x : I = ∫_0 ^π ((π−u)/((a^2 cos^2 u+b^2 sin^2 u)^2 )) du ⇒ 2I = ∫_0 ^π (π/((a^2 cos^2 u+b^2 sin^2 u)^2 )) du ⇒ I = (π/2)∫_0 ^π (du/(a^4 cos^4 u(1+(b^2 /a^2 )tan^2 u)^2 )) I = π∫_0 ^(π/2) (du/(a^4 cos^4 u(1+(b^2 /a^2 )tan^2 u)^2 )) Let t = tanu : I = π∫_0 ^∞ ((dt/(1+t^2 ))/(a^4 (1/((1+t^2 )^2 ))(1+(b^2 /a^2 )t^2 )^2 )) I = (π/a^4 )∫_0 ^∞ ((1+t^2 )/((1+(b^2 /a^2 )t^2 )^2 )) dt I = (π/(a^2 b^2 ))∫_0 ^∞ (((b^2 /a^2 )+(b^2 /a^2 )t^2 )/((1+(b^2 /a^2 )t^2 )^2 )) dt I = (π/(a^2 b^2 ))∫_0 ^∞ ((1/(1+(b^2 /a^2 )t^2 ))−((1−(b^2 /a^2 ))/((1+(b^2 /a^2 )t^2 )^2 ))) dt I = (π/(a^2 b^2 ))[(a/b)arctan((b/a)t)+((a^2 −b^2 )/2).(t/((a^2 +b^2 t^2 ))) +((a^2 −b^2 )/(2ab))arctan((b/a)t)]_0 ^∞ I = (π/(a^2 b^2 ))((π/2).(a/b)+0+(π/2).((a^2 −b^2 )/(2ab))) I = ((π^2 (3a^2 −b^2 ))/(4a^3 b^3 ))](Q151439.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi} \frac{{x}}{\left({a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:\pi−{x}\:: \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\pi} \frac{\pi−{u}}{\left({a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} {u}+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} {u}\right)^{\mathrm{2}} }\:{du} \\ $$$$\Rightarrow\:\mathrm{2I}\:=\:\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\left({a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} {u}+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} {u}\right)^{\mathrm{2}} }\:{du} \\ $$$$\Rightarrow\:\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \frac{{du}}{{a}^{\mathrm{4}} \mathrm{cos}^{\mathrm{4}} {u}\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mathrm{tan}^{\mathrm{2}} {u}\right)^{\mathrm{2}} } \\ $$$$\:\mathrm{I}\:=\:\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{du}}{{a}^{\mathrm{4}} \mathrm{cos}^{\mathrm{4}} {u}\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mathrm{tan}^{\mathrm{2}} {u}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Let}\:{t}\:=\:\mathrm{tan}{u}\:: \\ $$$$\mathrm{I}\:=\:\pi\int_{\mathrm{0}} ^{\infty} \frac{\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }}{{a}^{\mathrm{4}} \frac{\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\frac{\pi}{{a}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+{t}^{\mathrm{2}} }{\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dt} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \frac{\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} }{\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dt} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} }−\frac{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)\:{dt} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\left[\frac{{a}}{{b}}\mathrm{arctan}\left(\frac{{b}}{{a}}{t}\right)+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}}.\frac{{t}}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}\right. \\ $$$$\left.+\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ab}}\mathrm{arctan}\left(\frac{{b}}{{a}}{t}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\left(\frac{\pi}{\mathrm{2}}.\frac{{a}}{{b}}+\mathrm{0}+\frac{\pi}{\mathrm{2}}.\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ab}}\right) \\ $$$$\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} \left(\mathrm{3}{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\mathrm{4}{a}^{\mathrm{3}} {b}^{\mathrm{3}} } \\ $$
