Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 52947 by gunawan last updated on 15/Jan/19

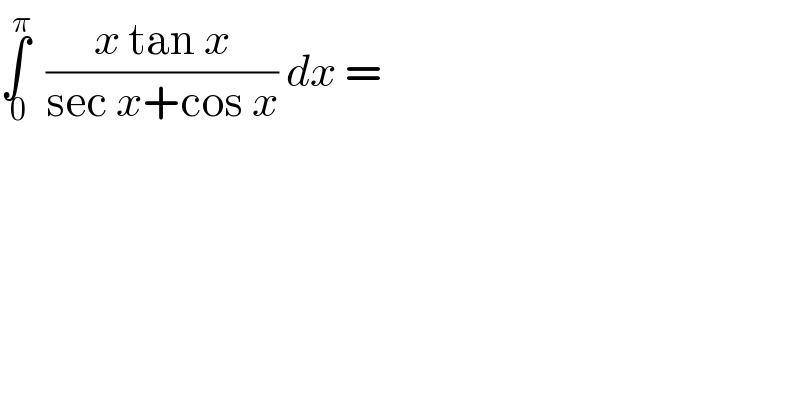
∫_( 0) ^π ((x tan x)/(sec x+cos x)) dx =

$$\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\frac{{x}\:\mathrm{tan}\:{x}}{\mathrm{sec}\:{x}+\mathrm{cos}\:{x}}\:{dx}\:= \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19

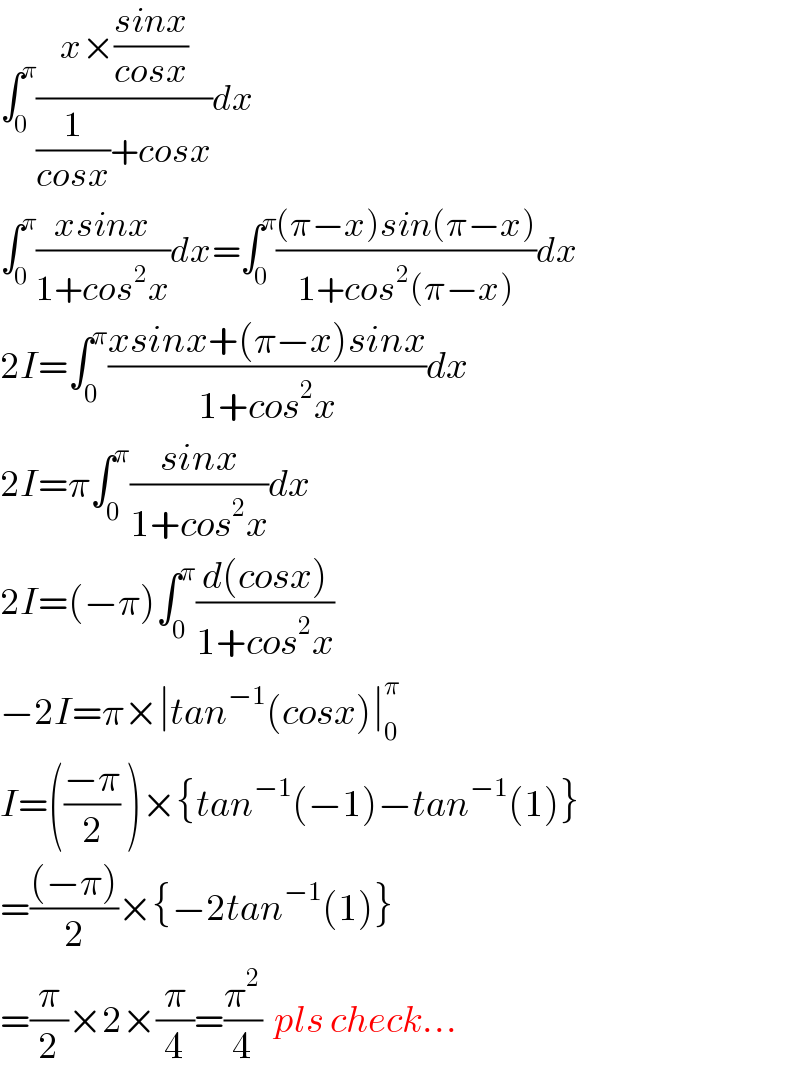
∫_0 ^π ((x×((sinx)/(cosx)))/((1/(cosx))+cosx))dx ∫_0 ^π ((xsinx)/(1+cos^2 x))dx=∫_0 ^π (((π−x)sin(π−x))/(1+cos^2 (π−x)))dx 2I=∫_0 ^π ((xsinx+(π−x)sinx)/(1+cos^2 x))dx 2I=π∫_0 ^π ((sinx)/(1+cos^2 x))dx 2I=(−π)∫_0 ^π ((d(cosx))/(1+cos^2 x)) −2I=π×∣tan^(−1) (cosx)∣_0 ^π I=(((−π)/2) )×{tan^(−1) (−1)−tan^(−1) (1)} =(((−π))/2)×{−2tan^(−1) (1)} =(π/2)×2×(π/4)=(π^2 /4) pls check...

$$\int_{\mathrm{0}} ^{\pi} \frac{{x}×\frac{{sinx}}{{cosx}}}{\frac{\mathrm{1}}{{cosx}}+{cosx}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{xsinx}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{x}\right){sin}\left(\pi−{x}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left(\pi−{x}\right)}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{{xsinx}+\left(\pi−{x}\right){sinx}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\mathrm{2}{I}=\pi\int_{\mathrm{0}} ^{\pi} \frac{{sinx}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\mathrm{2}{I}=\left(−\pi\right)\int_{\mathrm{0}} ^{\pi} \frac{{d}\left({cosx}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} {x}} \\ $$$$−\mathrm{2}{I}=\pi×\mid{tan}^{−\mathrm{1}} \left({cosx}\right)\mid_{\mathrm{0}} ^{\pi} \\ $$$${I}=\left(\frac{−\pi}{\mathrm{2}}\:\right)×\left\{{tan}^{−\mathrm{1}} \left(−\mathrm{1}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)\right\} \\ $$$$=\frac{\left(−\pi\right)}{\mathrm{2}}×\left\{−\mathrm{2}{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}×\mathrm{2}×\frac{\pi}{\mathrm{4}}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\:{pls}\:{check}... \\ $$

Commented by gunawan last updated on 16/Jan/19

Good bless you Sir

$$\mathrm{Good}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com