Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 210326 by Shrodinger last updated on 06/Aug/24

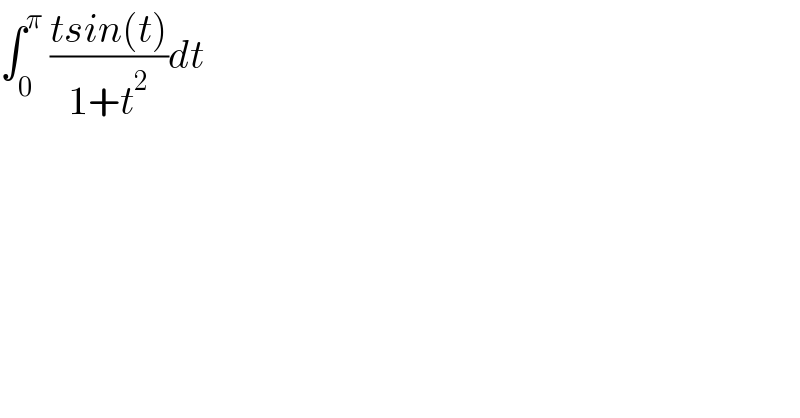
∫_0 ^π ((tsin(t))/(1+t^2 ))dt

$$\int_{\mathrm{0}} ^{\pi} \:\frac{{tsin}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$

Commented by Spillover last updated on 06/Aug/24

i got 1.6583 is it right?

$${i}\:{got}\:\mathrm{1}.\mathrm{6583}\:\:{is}\:{it}\:{right}? \\ $$

Commented by Shrodinger last updated on 06/Aug/24

no sir 0,20...

$${no}\:{sir}\:\mathrm{0},\mathrm{20}... \\ $$

Commented by Ghisom last updated on 07/Aug/24

≈.841492

$$\approx.\mathrm{841492} \\ $$

Commented by Frix last updated on 07/Aug/24

∫_0 ^π ((tcos t)/(t^2 +1))dt+i∫_0 ^π ((tsin t)/(t^2 +1))dt=∫_0 ^π ((te^(it) )/(t^2 +1))dt ⇒ ∫_0 ^π ((tsin t)/(t^2 +1))dt=imag (∫_0 ^π ((te^(it) )/(t^2 +1))dt) ...but I′m not good at this. Anyway we can get the exact result for ∫_(−∞) ^(+∞) ((tsin t)/(t^2 +1))dt=(π/e) using contour integration.

$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{t}\mathrm{cos}\:{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}+\mathrm{i}\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{t}\mathrm{sin}\:{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{te}^{{it}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{t}\mathrm{sin}\:{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\mathrm{imag}\:\left(\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{te}^{{it}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\right) \\ $$$$...\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{good}\:\mathrm{at}\:\mathrm{this}. \\ $$$$ \\ $$$$\mathrm{Anyway}\:\mathrm{we}\:\mathrm{can}\:\mathrm{get}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{result}\:\mathrm{for} \\ $$$$\underset{−\infty} {\overset{+\infty} {\int}}\:\frac{{t}\mathrm{sin}\:{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\frac{\pi}{\mathrm{e}} \\ $$$$\mathrm{using}\:\mathrm{contour}\:\mathrm{integration}. \\ $$

Commented by mahdipoor last updated on 07/Aug/24

This site can solve many integrals for example it has solved this integral with the help of imaginary numbers and ci and si functions. www.integral−calculator.com

$$ \\ $$$$\mathrm{This}\:\mathrm{site}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{many}\:\mathrm{integrals}\:\mathrm{for} \\ $$$$\mathrm{example}\:\mathrm{it}\:\mathrm{has}\:\mathrm{solved}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{help}\:\mathrm{of}\:\mathrm{imaginary}\:\mathrm{numbers}\:\mathrm{and}\:\mathrm{ci}\:\mathrm{and}\:\mathrm{si} \\ $$$$\mathrm{functions}. \\ $$$$\mathrm{www}.\mathrm{integral}−\mathrm{calculator}.\mathrm{com} \\ $$

Commented by Frix last updated on 07/Aug/24

Yes, I also found this site but there′s no useable exact solution, we must approximate at the end.

$$\mathrm{Yes},\:\mathrm{I}\:\mathrm{also}\:\mathrm{found}\:\mathrm{this}\:\mathrm{site}\:\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{no} \\ $$$$\mathrm{useable}\:\mathrm{exact}\:\mathrm{solution},\:\mathrm{we}\:\mathrm{must}\:\mathrm{approximate} \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{end}. \\ $$

Answered by Berbere last updated on 08/Aug/24

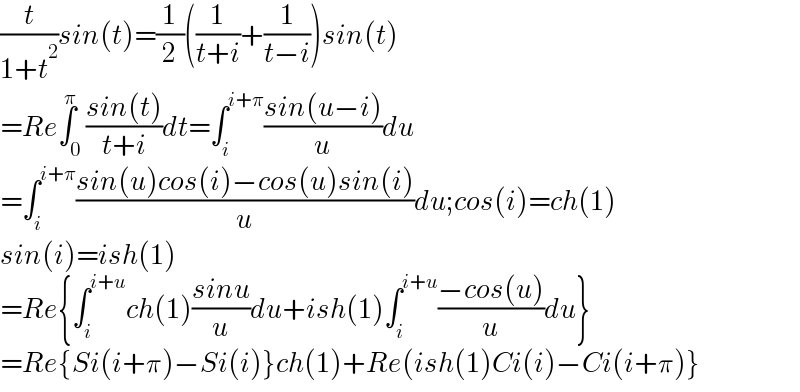
(t/(1+t^2 ))sin(t)=(1/2)((1/(t+i))+(1/(t−i)))sin(t) =Re∫_0 ^π ((sin(t))/(t+i))dt=∫_i ^(i+π) ((sin(u−i))/u)du =∫_i ^(i+π) ((sin(u)cos(i)−cos(u)sin(i))/u)du;cos(i)=ch(1) sin(i)=ish(1) =Re{∫_i ^(i+u) ch(1)((sinu)/u)du+ish(1)∫_i ^(i+u) ((−cos(u))/u)du} =Re{Si(i+π)−Si(i)}ch(1)+Re(ish(1)Ci(i)−Ci(i+π)}

$$\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{sin}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{t}+{i}}+\frac{\mathrm{1}}{{t}−{i}}\right){sin}\left({t}\right) \\ $$$$={Re}\overset{\pi} {\int}_{\mathrm{0}} \frac{{sin}\left({t}\right)}{{t}+{i}}{dt}=\int_{{i}} ^{{i}+\pi} \frac{{sin}\left({u}−{i}\right)}{{u}}{du} \\ $$$$=\int_{{i}} ^{{i}+\pi} \frac{{sin}\left({u}\right){cos}\left({i}\right)−{cos}\left({u}\right){sin}\left({i}\right)}{{u}}{du};{cos}\left({i}\right)={ch}\left(\mathrm{1}\right) \\ $$$${sin}\left({i}\right)={ish}\left(\mathrm{1}\right) \\ $$$$={Re}\left\{\int_{{i}} ^{{i}+{u}} {ch}\left(\mathrm{1}\right)\frac{{sinu}}{{u}}{du}+{ish}\left(\mathrm{1}\right)\int_{{i}} ^{{i}+{u}} \frac{−{cos}\left({u}\right)}{{u}}{du}\right\} \\ $$$$={Re}\left\{{Si}\left({i}+\pi\right)−{Si}\left({i}\right)\right\}{ch}\left(\mathrm{1}\right)+{Re}\left({ish}\left(\mathrm{1}\right){Ci}\left({i}\right)−{Ci}\left({i}+\pi\right)\right\} \\ $$

Commented by hardmath last updated on 11/Aug/24

Dear professor, your solutions are perfect

$$ \\ $$Dear professor, your solutions are perfect

Terms of Service

Privacy Policy

Contact: info@tinkutara.com