
Question Number 139883 by qaz last updated on 02/May/21

$$\int_{\mathrm{0}} ^{\pi} \mathrm{sin}\:^{\mathrm{2}{n}} {xdx}=? \\ $$
Answered by Dwaipayan Shikari last updated on 02/May/21
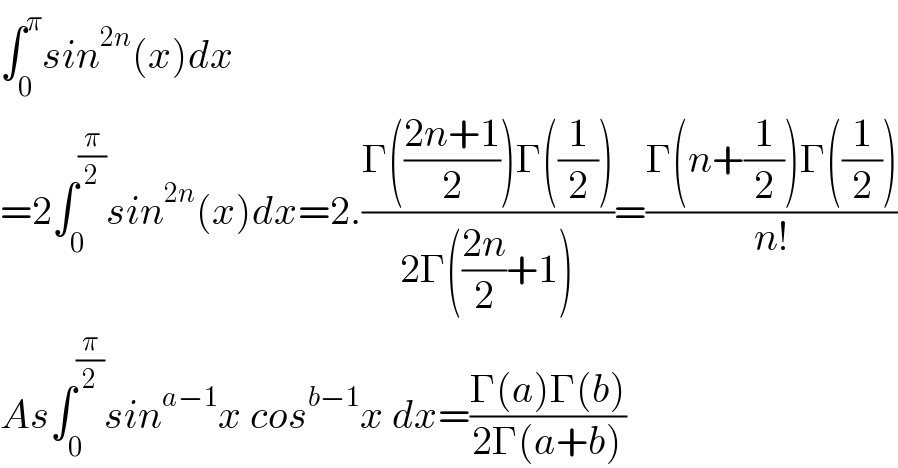
$$\int_{\mathrm{0}} ^{\pi} {sin}^{\mathrm{2}{n}} \left({x}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{n}} \left({x}\right){dx}=\mathrm{2}.\frac{\Gamma\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{\mathrm{2}{n}}{\mathrm{2}}+\mathrm{1}\right)}=\frac{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{{n}!} \\ $$$${As}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{{a}−\mathrm{1}} {x}\:{cos}^{{b}−\mathrm{1}} {x}\:{dx}=\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{\mathrm{2}\Gamma\left({a}+{b}\right)} \\ $$
Commented by Ar Brandon last updated on 02/May/21

$$=\frac{\pi\mathrm{n}\left(\mathrm{2n}−\mathrm{1}\right)!}{\mathrm{2}^{\mathrm{2n}−\mathrm{1}} \left(\mathrm{n}!\right)^{\mathrm{2}} } \\ $$
