
Question Number 116216 by bemath last updated on 02/Oct/20
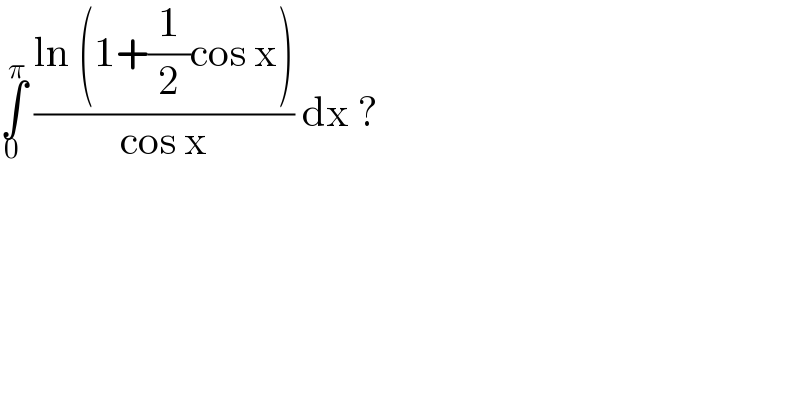
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{ln}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:? \\ $$
Answered by Bird last updated on 02/Oct/20

$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{ln}\left(\mathrm{1}+{acosx}\right)}{{cosx}}{dx}\:{with}−\mathrm{1}<{a}<\mathrm{1} \\ $$$$ \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{\mathrm{1}+{acosx}} \\ $$$$=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}.\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +{a}−{at}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\left(\mathrm{1}−{a}\right){t}^{\mathrm{2}} \:+\mathrm{1}+{a}} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{1}−{a}\right)}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}} \\ $$$$=_{{t}=\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}+{a}}}{u}} \:\:\:\frac{\mathrm{2}}{\mathrm{1}−{a}}.\frac{\mathrm{1}−{a}}{\mathrm{1}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}.\frac{\sqrt{\mathrm{1}+{a}}}{\mathrm{1}−{a}}{u} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}.\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\int\:\:\frac{\pi}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{da}\:+{c} \\ $$$$=\pi\:{arcsina}\:+{c} \\ $$$${f}\left(\mathrm{0}\right)\:=\mathrm{0}={c}\:\Rightarrow{f}\left({a}\right)\:=\pi\:{arcsin}\left({a}\right) \\ $$$${and}\:\int_{\mathrm{0}} ^{\pi} \:\frac{{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{cosx}\right)}{{cosx}}{dx} \\ $$$$={f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\pi\:{arcsin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$
Commented by bemath last updated on 02/Oct/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mnjuly1970 last updated on 02/Oct/20
$${very}\:{nice}\:{solution}\:.{thank}\:{you}\: \\ $$$${mr}\:{bird}.. \\ $$
Commented by mathmax by abdo last updated on 02/Oct/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
