
Question Number 140930 by bramlexs22 last updated on 14/May/21
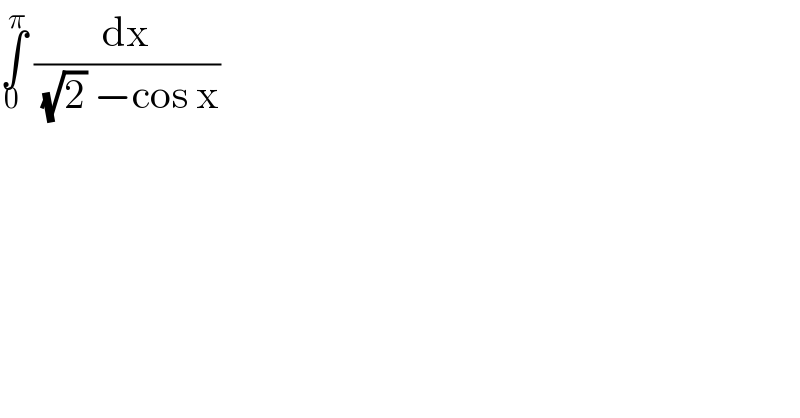
$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{2}}\:−\mathrm{cos}\:\mathrm{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 14/May/21
![2∫_0 ^∞ (dt/( (√2)−((1−t^2 )/(1+t^2 )))).(1/(1+t^2 )) t=tan(x/2) =2∫_0 ^∞ (dt/( (√2)t^2 +(√2)−1+t^2 ))dt=(1/( (√2)+1))∫_(−∞) ^∞ (dt/(t^2 +(((√2)−1)/( (√2)+1))))dt =(1/( (√2)+1)).(√((((√2)+1)/( (√2)−1))[)) tan^(−1) (t(√(((√2)+1)/( (√2)−1))))]_(−∞) ^∞ dx =π](Q140931.png)
$$\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\:\sqrt{\mathrm{2}}−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:{t}={tan}\frac{{x}}{\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\:\sqrt{\mathrm{2}}{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}−\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\int_{−\infty} ^{\infty} \frac{{dt}}{{t}^{\mathrm{2}} +\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}}{dt} \\ $$$$\left.=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}.\sqrt{\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\left[\right.}\:{tan}^{−\mathrm{1}} \left({t}\sqrt{\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}}\right)\right]_{−\infty} ^{\infty} {dx} \\ $$$$=\pi \\ $$
Commented by bramlexs22 last updated on 14/May/21

$$\mathrm{Weirrstrass}\:\mathrm{substitution} \\ $$
Commented by Dwaipayan Shikari last updated on 14/May/21

$${yes}! \\ $$
Answered by mathmax by abdo last updated on 14/May/21
![I=∫_0 ^π (dx/( (√2)−cosx)) we do the changement tan((x/2))=t ⇒ I =∫_0 ^∞ ((2dt)/((1+t^2 )((√2)−((1−t^2 )/(1+t^2 ))))) =2∫_0 ^∞ (dt/( (√2)+(√2)t^2 −1+t^2 )) =2∫_0 ^∞ (dt/((1+(√2))t^2 +(√2)−1)) =(2/(1+(√2)))∫_0 ^∞ (dt/(t^2 +(((√2)−1)/( (√2)+1)))) =(2/(1+(√2)))∫_0 ^∞ (dt/(t^2 +3−2(√2))) =_(t=(√(3−2(√2)))u) (2/(1+(√2))) ∫_0 ^∞ (((√(3−2(√2)))du)/((3−2(√2))(1+u^2 ))) =(2/((1+(√2))(√(3−2(√2)))))[arctanu]_0 ^∞ =(π/((1+(√2))(√(3−2(√2)))))](Q140953.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{2}}−\mathrm{cosx}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\sqrt{\mathrm{2}}−\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}\mathrm{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}−\mathrm{1}}\:=\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}\:=_{\mathrm{t}=\sqrt{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{u}} \:\:\:\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{du}}{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}}\left[\mathrm{arctanu}\right]_{\mathrm{0}} ^{\infty} \:=\frac{\pi}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}} \\ $$
Commented by mathmax by abdo last updated on 14/May/21

$$\mathrm{but}\:\:\sqrt{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}}−\mathrm{1}\:\Rightarrow\:\mathrm{I}\:=\frac{\pi}{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}\:=\pi \\ $$$$ \\ $$
Answered by iloveisrael last updated on 14/May/21
![R=∫_0 ^π (dx/(a−cos x)) ; a>1 put μ = tan (x/2) R=∫_0 ^π ((1+μ^2 )/(a+aμ^2 −1+μ^2 )) . (2/(1+μ^2 )) dμ (∗) a−1+(1+a)μ^2 ; set ((a−1)/(a+1)) = p^2 and μ=pu R= (2/(a+1)) ∫_0 ^( ∞) (p/(p^2 (1+u^2 ))) du R= (2/( (√(a^2 −1)))) [ arctan u ] _0^∞ R= (2/( (√(a^2 −1)))) .(π/2) = (π/( (√(a^2 −1)))) R= (π/( (√(((√2))^2 −1)))) = π](Q140960.png)
$$\:{R}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{dx}}{{a}−\mathrm{cos}\:{x}}\:;\:{a}>\mathrm{1} \\ $$$${put}\:\mu\:=\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\: \\ $$$$\:{R}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\mathrm{1}+\mu^{\mathrm{2}} }{{a}+{a}\mu^{\mathrm{2}} −\mathrm{1}+\mu^{\mathrm{2}} }\:.\:\frac{\mathrm{2}}{\mathrm{1}+\mu^{\mathrm{2}} }\:{d}\mu \\ $$$$\:\left(\ast\right)\:{a}−\mathrm{1}+\left(\mathrm{1}+{a}\right)\mu^{\mathrm{2}} \:;\:{set}\:\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\:=\:{p}^{\mathrm{2}} \\ $$$$\:{and}\:\mu={pu}\: \\ $$$$\:{R}=\:\frac{\mathrm{2}}{{a}+\mathrm{1}}\:\underset{\mathrm{0}} {\overset{\:\:\infty} {\int}}\:\frac{{p}}{{p}^{\mathrm{2}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:{du} \\ $$$$\:{R}=\:\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\:\left[\:\mathrm{arctan}\:\:{u}\:\right]\:_{\mathrm{0}} ^{\infty} \\ $$$$\:{R}=\:\frac{\mathrm{2}}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\:.\frac{\pi}{\mathrm{2}}\:=\:\frac{\pi}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\:{R}=\:\frac{\pi}{\:\sqrt{\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}}}\:=\:\pi\: \\ $$
