
Question Number 165741 by metamorfose last updated on 07/Feb/22
![∫_0 ^π (dt/(1−sina.cost))=??? , a∈]0,(π/2)[](Q165741.png)
$$\left.\int_{\mathrm{0}} ^{\pi} \frac{{dt}}{\mathrm{1}−{sina}.{cost}}=???\:,\:{a}\in\right]\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\right. \\ $$
Answered by MJS_new last updated on 08/Feb/22
![a∈]0; (π/2)[ ⇒ 0<sin a <1 ⇒ let sin a =A; 0<A<1 ∫(dt/(1−Acos t))= [u=tan (t/2) ⇒ dt=((2du)/(u^2 +1))] =2∫(du/((1+A)u^2 +(1−A)))= [let B=1+A ∧ C=1−A ⇒ B, C >0] =2∫(du/(Bu^2 +C))= [u=((√C)/( (√B)))v → du=((√C)/( (√B)))dv] =(2/( (√(BC))))∫(dv/(v^2 +1))=(2/( (√(BC))))arctan v = =(2/( (√(1−A^2 ))))arctan (((√(1+A)) u)/( (√(1−A)))) = =(2/(cos a))arctan (((√(1+sin a)) tan (t/2))/( (√(1−sin a)))) +C ⇒ answer is lim_(t→π^− ) ((2/(cos a))arctan (((√(1+sin a)) tan (t/2))/( (√(1−sin a))))) =(π/(cos a))](Q165763.png)
$$\left.{a}\in\right]\mathrm{0};\:\frac{\pi}{\mathrm{2}}\left[\:\Rightarrow\:\mathrm{0}<\mathrm{sin}\:{a}\:<\mathrm{1}\:\Rightarrow\:\mathrm{let}\:\mathrm{sin}\:{a}\:={A};\:\mathrm{0}<{A}<\mathrm{1}\right. \\ $$$$\int\frac{{dt}}{\mathrm{1}−{A}\mathrm{cos}\:{t}}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\:\Rightarrow\:{dt}=\frac{\mathrm{2}{du}}{{u}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\mathrm{2}\int\frac{{du}}{\left(\mathrm{1}+{A}\right){u}^{\mathrm{2}} +\left(\mathrm{1}−{A}\right)}= \\ $$$$\:\:\:\:\:\left[\mathrm{let}\:{B}=\mathrm{1}+{A}\:\wedge\:{C}=\mathrm{1}−{A}\:\Rightarrow\:{B},\:{C}\:>\mathrm{0}\right] \\ $$$$=\mathrm{2}\int\frac{{du}}{{Bu}^{\mathrm{2}} +{C}}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{{C}}}{\:\sqrt{{B}}}{v}\:\rightarrow\:{du}=\frac{\sqrt{{C}}}{\:\sqrt{{B}}}{dv}\right] \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{{BC}}}\int\frac{{dv}}{{v}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{2}}{\:\sqrt{{BC}}}\mathrm{arctan}\:{v}\:= \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{A}^{\mathrm{2}} }}\mathrm{arctan}\:\frac{\sqrt{\mathrm{1}+\mathrm{A}}\:{u}}{\:\sqrt{\mathrm{1}−{A}}}\:= \\ $$$$=\frac{\mathrm{2}}{\mathrm{cos}\:{a}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{1}+\mathrm{sin}\:{a}}\:\mathrm{tan}\:\frac{{t}}{\mathrm{2}}}{\:\sqrt{\mathrm{1}−\mathrm{sin}\:{a}}}\:+{C} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\underset{{t}\rightarrow\pi^{−} } {\mathrm{lim}}\:\left(\frac{\mathrm{2}}{\mathrm{cos}\:{a}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{1}+\mathrm{sin}\:{a}}\:\mathrm{tan}\:\frac{{t}}{\mathrm{2}}}{\:\sqrt{\mathrm{1}−\mathrm{sin}\:{a}}}\right)\:=\frac{\pi}{\mathrm{cos}\:{a}} \\ $$
Commented by metamorfose last updated on 09/Feb/22

$${thnx}\:{sir} \\ $$
Answered by Mathspace last updated on 08/Feb/22
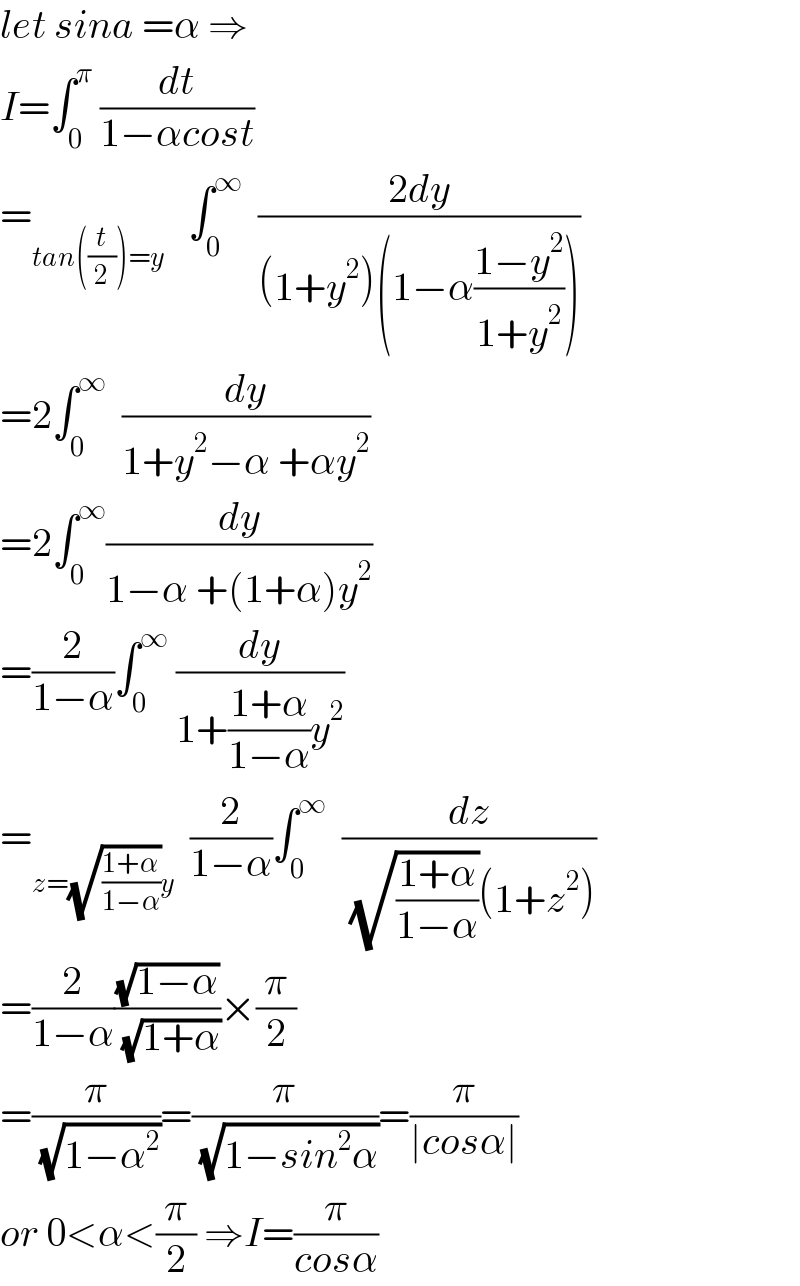
$${let}\:{sina}\:=\alpha\:\Rightarrow \\ $$$${I}=\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{\mathrm{1}−\alpha{cost}} \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={y}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dy}}{\left(\mathrm{1}+{y}^{\mathrm{2}} \right)\left(\mathrm{1}−\alpha\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} −\alpha\:+\alpha{y}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{dy}}{\mathrm{1}−\alpha\:+\left(\mathrm{1}+\alpha\right){y}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\alpha}\int_{\mathrm{0}} ^{\infty} \:\frac{{dy}}{\mathrm{1}+\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}{y}^{\mathrm{2}} } \\ $$$$=_{{z}=\sqrt{\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}}{y}} \:\:\frac{\mathrm{2}}{\mathrm{1}−\alpha}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dz}}{\:\sqrt{\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\alpha}\frac{\sqrt{\mathrm{1}−\alpha}}{\:\sqrt{\mathrm{1}+\alpha}}×\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} }}=\frac{\pi}{\:\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \alpha}}=\frac{\pi}{\mid{cos}\alpha\mid} \\ $$$${or}\:\mathrm{0}<\alpha<\frac{\pi}{\mathrm{2}}\:\Rightarrow{I}=\frac{\pi}{{cos}\alpha} \\ $$
Commented by metamorfose last updated on 09/Feb/22

$${thnx}\:{sir} \\ $$
Commented by Mathspace last updated on 08/Feb/22

$${I}=\frac{\pi}{{cosa}} \\ $$
