
Question Number 65100 by arcana last updated on 25/Jul/19
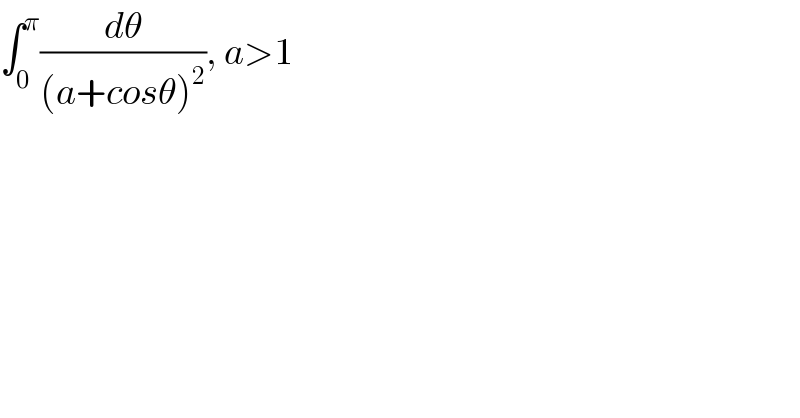
$$\int_{\mathrm{0}} ^{\pi} \frac{{d}\theta}{\left({a}+{cos}\theta\right)^{\mathrm{2}} },\:{a}>\mathrm{1} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19
![let g(a)=∫_0 ^π (dθ/(a+cosθ )) then ∫_0 ^π (dθ/((a+cosθ)^2 ))=−(dg/(da )) so let find g(a) g(a)=∫_0 ^π (dθ/((a−1)+2cos^2 ((θ/2))))=∫_0 ^(π/2) ((2dx)/((a−1)[cos^2 x+sin^2 x]+2cos^2 x))=2∫_0 ^(π/2) (dx/((a+1)cos^2 x +(a−1)sin^2 x)) then ((g(a))/2)= ∫_0 ^(π/2) (((1/(cos^2 x)) dx)/((a+1)+(a−1)tan^2 x)) we have a>1⇒(a+1)+(a−1)tan^2 x=(a+1)[1+((√((a−1)/(a+1)))tanx)^2 ] ((g(a))/2)=(1/(√(a^2 −1)))∫_0 ^(π/2) (((√((a−1)/(a+1))) (1+tan^2 x) dx)/(1+((√(((a−1)/(a+1)) )) tanx)^2 )) So we get g(a)=(2/(√(a^2 −1))) [arctan((√(((a−1)/(a+1)) )) tanx)]_0 ^(π/2) = (π/(√(a^2 −1))) then (dg/da)=π.((((−2a)/(2(√(a^2 −1))))/(a^2 −1)))= ((−πa)/((a^2 −1)^(3/2) )) that leads us to ∫_(0 ) ^π (dθ/((a+cosθ)^2 )) = ((πa)/((a^2 −1)^(3/2) ))](Q65104.png)
$${let}\:\:{g}\left({a}\right)=\int_{\mathrm{0}} ^{\pi} \frac{{d}\theta}{{a}+{cos}\theta\:}\:\:\:{then}\:\:\int_{\mathrm{0}} ^{\pi} \frac{{d}\theta}{\left({a}+{cos}\theta\right)^{\mathrm{2}} }=−\frac{{dg}}{{da}\:\:}\:\:\:\:\:\:{so}\:{let}\:{find}\:{g}\left({a}\right) \\ $$$${g}\left({a}\right)=\int_{\mathrm{0}} ^{\pi} \frac{{d}\theta}{\left({a}−\mathrm{1}\right)+\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{dx}}{\left({a}−\mathrm{1}\right)\left[{cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right]+\mathrm{2}{cos}^{\mathrm{2}} {x}}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\left({a}+\mathrm{1}\right){cos}^{\mathrm{2}} {x}\:+\left({a}−\mathrm{1}\right){sin}^{\mathrm{2}} {x}} \\ $$$${then} \\ $$$$\frac{{g}\left({a}\right)}{\mathrm{2}}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\:{dx}}{\left({a}+\mathrm{1}\right)+\left({a}−\mathrm{1}\right){tan}^{\mathrm{2}} {x}}\: \\ $$$${we}\:{have}\:{a}>\mathrm{1}\Rightarrow\left({a}+\mathrm{1}\right)+\left({a}−\mathrm{1}\right){tan}^{\mathrm{2}} {x}=\left({a}+\mathrm{1}\right)\left[\mathrm{1}+\left(\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}{tanx}\right)^{\mathrm{2}} \right] \\ $$$$\frac{{g}\left({a}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:{dx}}{\mathrm{1}+\left(\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\:}\:{tanx}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:{So}\:\:\:{we}\:{get} \\ $$$${g}\left({a}\right)=\frac{\mathrm{2}}{\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\:\left[{arctan}\left(\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\:\:}\:{tanx}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\:\frac{\pi}{\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\: \\ $$$${then}\:\:\frac{{dg}}{{da}}=\pi.\left(\frac{\frac{−\mathrm{2}{a}}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}}{{a}^{\mathrm{2}} −\mathrm{1}}\right)=\:\frac{−\pi{a}}{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$ \\ $$$${that}\:{leads}\:{us}\:{to} \\ $$$$\int_{\mathrm{0}\:} ^{\pi} \:\frac{{d}\theta}{\left({a}+{cos}\theta\right)^{\mathrm{2}} }\:=\:\frac{\pi{a}}{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:\: \\ $$
Commented by turbo msup by abdo last updated on 25/Jul/19
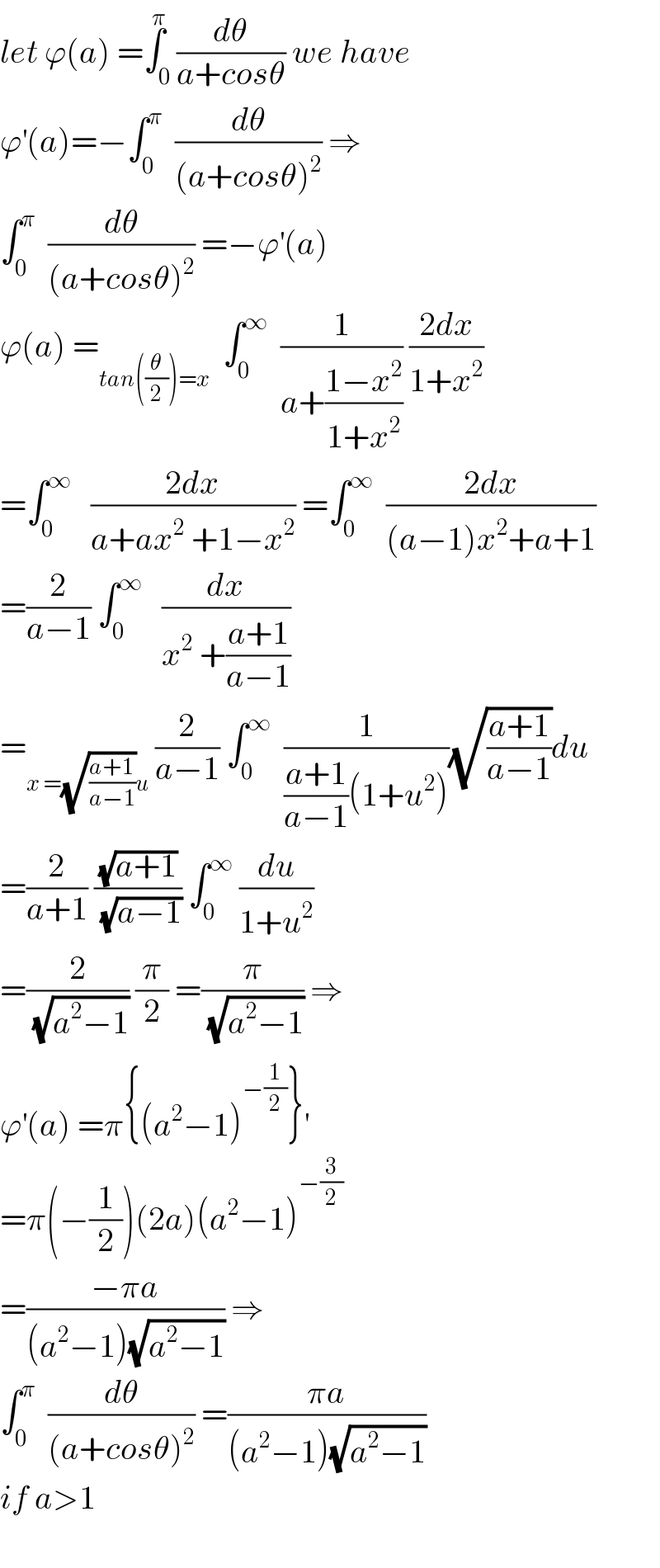
$${let}\:\varphi\left({a}\right)\:=\overset{\pi} {\int}_{\mathrm{0}} \frac{{d}\theta}{{a}+{cos}\theta}\:{we}\:{have} \\ $$$$\varphi^{'} \left({a}\right)=−\int_{\mathrm{0}} ^{\pi} \:\:\frac{{d}\theta}{\left({a}+{cos}\theta\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\frac{{d}\theta}{\left({a}+{cos}\theta\right)^{\mathrm{2}} }\:=−\varphi^{'} \left({a}\right) \\ $$$$\varphi\left({a}\right)\:=_{{tan}\left(\frac{\theta}{\mathrm{2}}\right)={x}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{dx}}{{a}+{ax}^{\mathrm{2}} \:+\mathrm{1}−{x}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dx}}{\left({a}−\mathrm{1}\right){x}^{\mathrm{2}} +{a}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{{a}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}} \\ $$$$=_{{x}\:=\sqrt{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}}{u}} \:\frac{\mathrm{2}}{{a}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\sqrt{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}}{du} \\ $$$$=\frac{\mathrm{2}}{{a}+\mathrm{1}}\:\frac{\sqrt{{a}+\mathrm{1}}}{\sqrt{{a}−\mathrm{1}}}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\:\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow \\ $$$$\varphi^{'} \left({a}\right)\:=\pi\left\{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{'} \\ $$$$=\pi\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{2}{a}\right)\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$=\frac{−\pi{a}}{\left({a}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\frac{{d}\theta}{\left({a}+{cos}\theta\right)^{\mathrm{2}} }\:=\frac{\pi{a}}{\left({a}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${if}\:{a}>\mathrm{1} \\ $$$$ \\ $$
Commented by arcana last updated on 25/Jul/19

$$\mathrm{Gracias} \\ $$
Commented by arcana last updated on 25/Jul/19

$$\mathrm{Gracias} \\ $$
Commented by turbo msup by abdo last updated on 25/Jul/19

$${where}\:{are}\:{you}\:{from}\:{arcana}... \\ $$
Commented by arcana last updated on 25/Jul/19
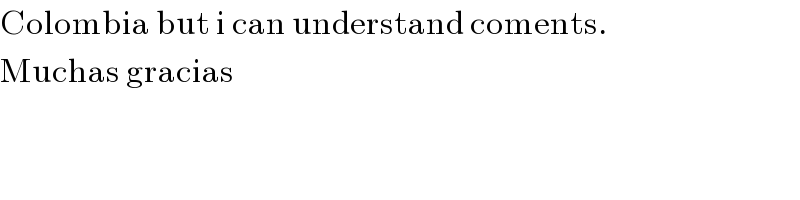
$$\mathrm{Colombia}\:\mathrm{but}\:\mathrm{i}\:\mathrm{can}\:\mathrm{understand}\:\mathrm{coments}. \\ $$$$\mathrm{Muchas}\:\mathrm{gracias} \\ $$
Commented by mathmax by abdo last updated on 25/Jul/19
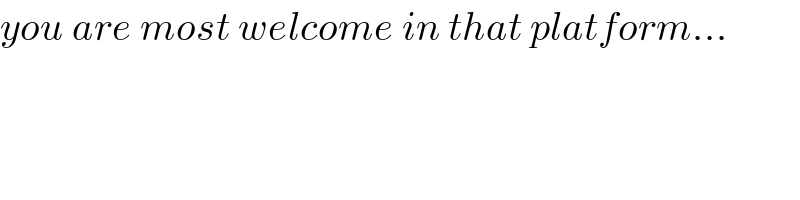
$${you}\:{are}\:{most}\:{welcome}\:{in}\:{that}\:{platform}... \\ $$
Commented by arcana last updated on 26/Jul/19

$$\mathrm{de}\:\mathrm{nuevo}\:\mathrm{gracias} \\ $$
