
Question Number 149023 by ArielVyny last updated on 02/Aug/21
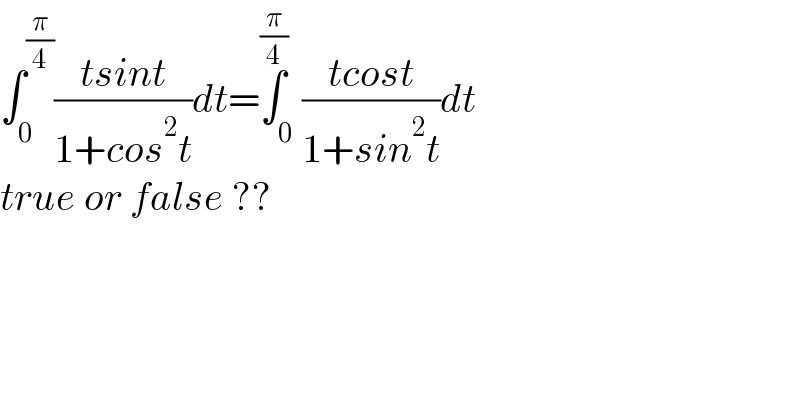
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{tsint}}{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}=\overset{\frac{\pi}{\mathrm{4}}} {\int}_{\mathrm{0}} \frac{{tcost}}{\mathrm{1}+{sin}^{\mathrm{2}} {t}}{dt} \\ $$$${true}\:{or}\:{false}\:?? \\ $$
Answered by mindispower last updated on 02/Aug/21
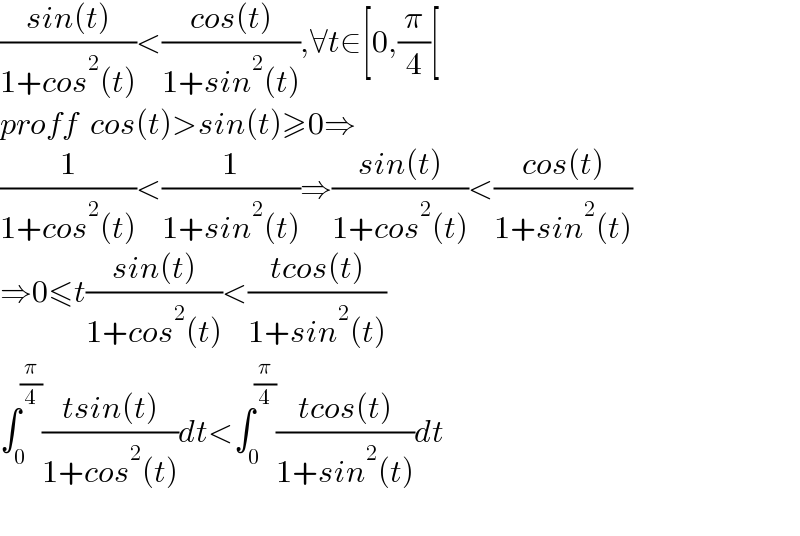
$$\frac{{sin}\left({t}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left({t}\right)}<\frac{{cos}\left({t}\right)}{\mathrm{1}+{sin}^{\mathrm{2}} \left({t}\right)},\forall{t}\in\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\left[\right.\right. \\ $$$${proff}\:\:{cos}\left({t}\right)>{sin}\left({t}\right)\geqslant\mathrm{0}\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{cos}^{\mathrm{2}} \left({t}\right)}<\frac{\mathrm{1}}{\mathrm{1}+{sin}^{\mathrm{2}} \left({t}\right)}\Rightarrow\frac{{sin}\left({t}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left({t}\right)}<\frac{{cos}\left({t}\right)}{\mathrm{1}+{sin}^{\mathrm{2}} \left({t}\right)} \\ $$$$\Rightarrow\mathrm{0}\leqslant{t}\frac{{sin}\left({t}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left({t}\right)}<\frac{{tcos}\left({t}\right)}{\mathrm{1}+{sin}^{\mathrm{2}} \left({t}\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{tsin}\left({t}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left({t}\right)}{dt}<\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{tcos}\left({t}\right)}{\mathrm{1}+{sin}^{\mathrm{2}} \left({t}\right)}{dt} \\ $$$$ \\ $$
Commented by mindispower last updated on 03/Aug/21
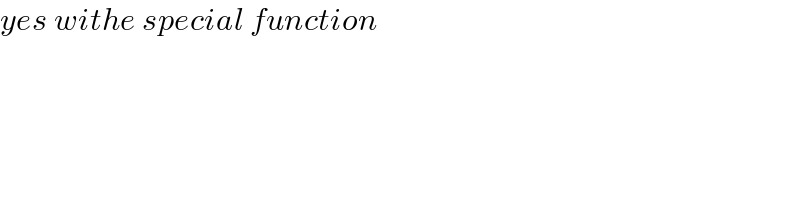
$${yes}\:{withe}\:{special}\:{function} \\ $$
Commented by ArielVyny last updated on 02/Aug/21
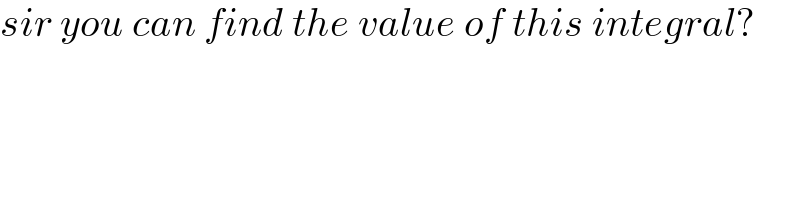
$${sir}\:{you}\:{can}\:{find}\:{the}\:{value}\:{of}\:{this}\:{integral}? \\ $$
Commented by ArielVyny last updated on 06/Aug/21
$${you}\:{can}\:{solve}\:{it}\:{please} \\ $$
