
Question Number 200685 by Spillover last updated on 21/Nov/23
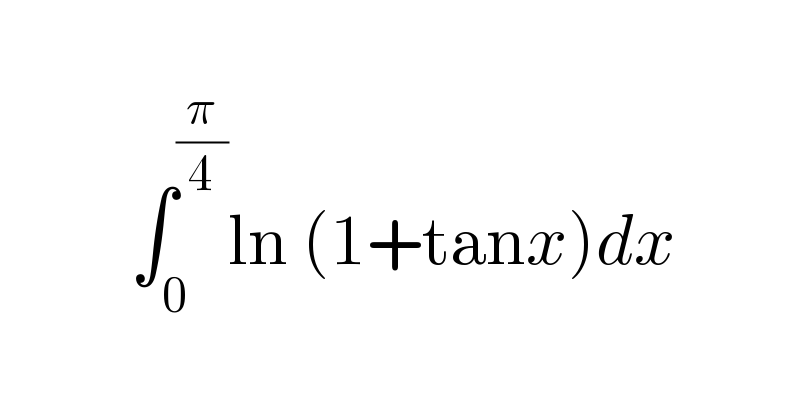
$$\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\:\left(\mathrm{1}+\mathrm{tan}{x}\right){dx}\: \\ $$$$ \\ $$
Answered by som(math1967) last updated on 22/Nov/23
![I=∫_0 ^(π/4) ln[1+tan((π/4)−x)]dx I=∫_0 ^(π/4) ln[1+((1−tanx)/(1+tanx))]dx I=∫_0 ^(π/4) ln((2/(1+tanx)))dx I=∫_0 ^(π/4) ln2dx−∫_0 ^(π/4) ln(1+tanx)dx I=∫_0 ^(π/4) ln2 dx−I 2I=ln2[x]_0 ^(π/4) I=(π/8)ln2](Q200690.png)
$$\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left[\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right]{dx} \\ $$$$\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left[\mathrm{1}+\frac{\mathrm{1}−{tanx}}{\mathrm{1}+{tanx}}\right]{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tanx}}\right){dx} \\ $$$$\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{2}{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tanx}\right){dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{2}\:{dx}−{I} \\ $$$$\mathrm{2}{I}={ln}\mathrm{2}\left[{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$\:{I}=\frac{\pi}{\mathrm{8}}{ln}\mathrm{2} \\ $$
