
Question Number 161660 by amin96 last updated on 20/Dec/21
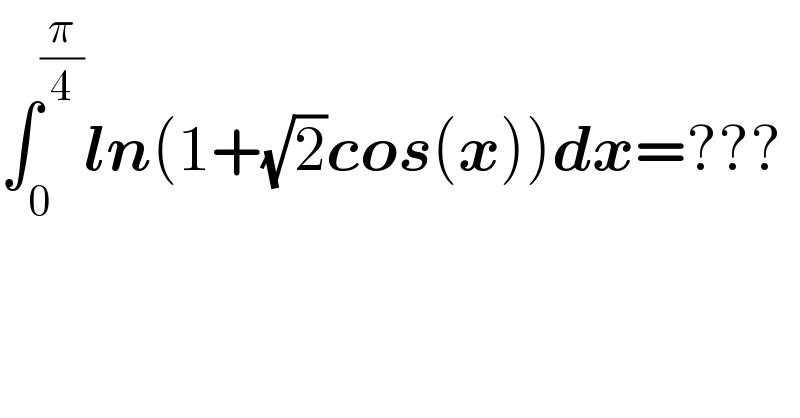
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \boldsymbol{{ln}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)\right)\boldsymbol{{dx}}=??? \\ $$
Answered by mindispower last updated on 21/Dec/21
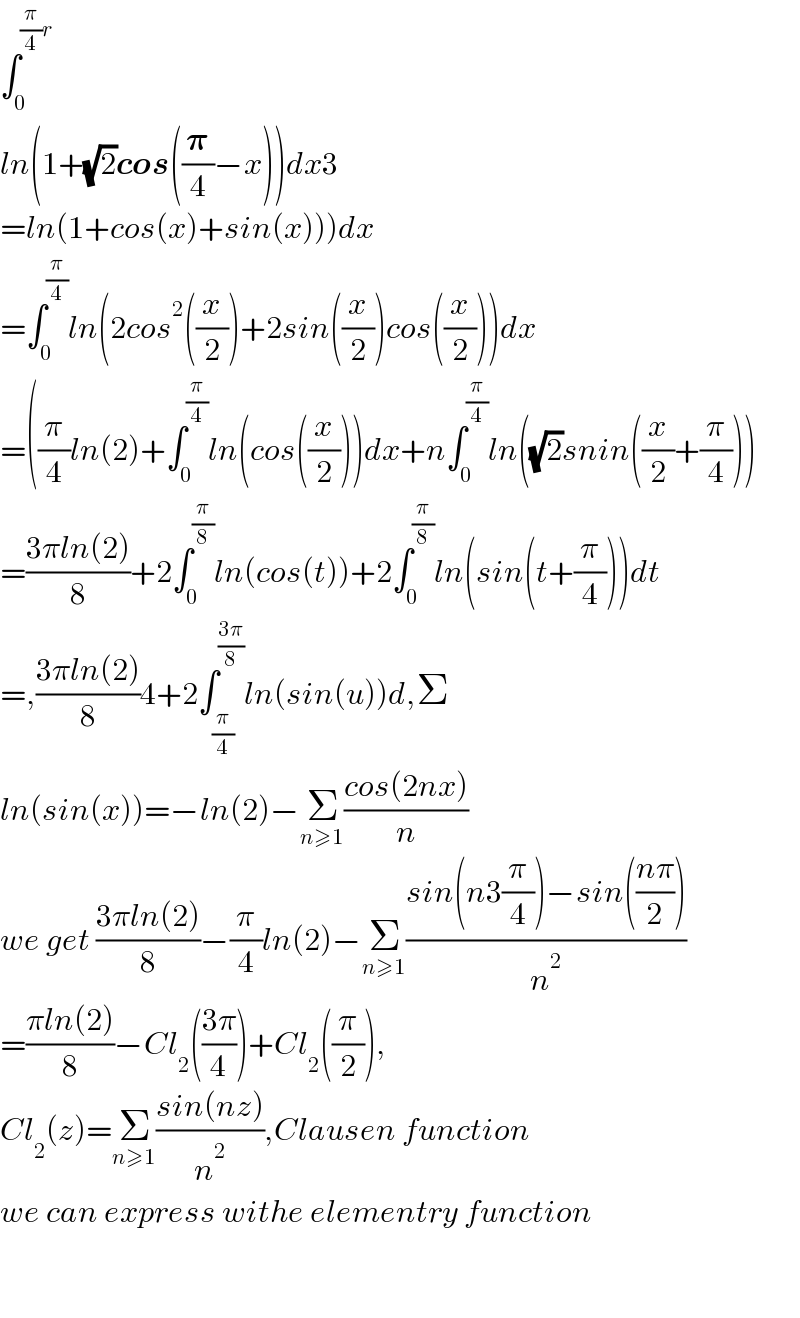
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}{r}} \\ $$$${ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\boldsymbol{{cos}}\left(\frac{\boldsymbol{\pi}}{\mathrm{4}}−{x}\right)\right){dx}\mathrm{3} \\ $$$$\left.={ln}\left(\mathrm{1}+{cos}\left({x}\right)+{sin}\left({x}\right)\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)\right){dx} \\ $$$$=\left(\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\frac{{x}}{\mathrm{2}}\right)\right){dx}+{n}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\sqrt{\mathrm{2}}{snin}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\right)\right. \\ $$$$=\frac{\mathrm{3}\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}}+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} {ln}\left({cos}\left({t}\right)\right)+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} {ln}\left({sin}\left({t}+\frac{\pi}{\mathrm{4}}\right)\right){dt} \\ $$$$=,\frac{\mathrm{3}\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\mathrm{4}+\mathrm{2}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{3}\pi}{\mathrm{8}}} {ln}\left({sin}\left({u}\right)\right){d},\Sigma \\ $$$${ln}\left({sin}\left({x}\right)\right)=−{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$${we}\:{get}\:\frac{\mathrm{3}\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}}−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({n}\mathrm{3}\frac{\pi}{\mathrm{4}}\right)−{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)}{{n}^{\mathrm{2}} } \\ $$$$=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}}−{Cl}_{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)+{Cl}_{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\right), \\ $$$${Cl}_{\mathrm{2}} \left({z}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({nz}\right)}{{n}^{\mathrm{2}} },{Clausen}\:{function} \\ $$$${we}\:{can}\:{express}\:{withe}\:{elementry}\:{function} \\ $$$$ \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 21/Dec/21

$$\mathrm{g}\acute {\mathrm{e}nial}\:! \\ $$
Answered by mathmax by abdo last updated on 21/Dec/21
![f(a)=∫_0 ^(π/4) ln(1+acosx)dx (a>1) f^′ (a)=∫_0 ^(π/4) ((cosx)/(1+acosx))dx =(1/a)∫_0 ^(π/4) ((1+acosx−1)/(1+acosx))dx =(π/(4a))−(1/a)∫_0 ^(π/4) (dx/(1+acosx)) changement tan((x/2))=t give ∫_0 ^(π/4) (dx/(1+acosx))=∫_0 ^((√2)−1) ((2dt)/((1+t^2 )(1+a((1−t^2 )/(1+t^2 ))))) =2∫_0 ^((√2)−1) (dt/(1+t^2 +a−at^2 ))=2∫_0 ^((√2)−1) (dt/((1−a)t^2 +1+a)) =−2∫_0 ^((√2)−1) (dt/((a−1)t^2 −(1+a)))=((−2)/(a−1))∫_0 ^((√2)−1) (dt/(t^2 −((a+1)/(a−1)))) =_(t=(√((a+1)/(a−1)))u) ((−2)/(a−1)) ∫_0 ^(((√2)−1)(√((a−1)/(a+1)))) ((√((a+1)/(a−1)))/(((a+1)/(a−1))(u^2 −1)))du =((a−1)/(a+1))×((√(a+1))/( (√(a−1))))×((−2)/(a−1))∫_0 ^(((√2)−1)(√((a−1)/(a+1)))) (du/(u^2 −1)) =((√(a−1))/( (√(a+1))))×((−2)/(a−1))∫... du =−(1/( (√(a^2 −1))))∫_0 ^(((√2)−1)(√((a−1)/(a+1)))) ((1/(u−1))−(1/(u+1)))du =(1/( (√(a^2 −1))))[ln∣((u+1)/(u−1))∣]_0 ^(((√2)−1)(√((a−1)/(a+1)))) =(1/( (√(a^2 −1)))){ln∣((((√2)−1)(√((a−1)/(a+1)))+1)/(((√2)−1)(√((a−1)/(a+1)))−1))∣} ⇒ f^′ (a)=(π/(4a)) −(1/(a(√(a^2 −1))))ln∣((((√2)−1)(√((a−1)/(a+1)))+1)/(((√2)−1)(√((a−1)/(a+1)))−1))∣ ⇒ f(a)=(π/4)lna−∫ (1/(a(√(a^2 −1))))ln(((((√2)−1)(√((a−1)/(a+1)))+1)/(((√2)−1)(√((a−1)/(a+1)))−1))) +C ...be continued...](Q161738.png)
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{acosx}\right)\mathrm{dx}\:\:\:\left(\mathrm{a}>\mathrm{1}\right) \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{cosx}}{\mathrm{1}+\mathrm{acosx}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}+\mathrm{acosx}−\mathrm{1}}{\mathrm{1}+\mathrm{acosx}}\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4a}}−\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{acosx}}\:\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\mathrm{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{acosx}}=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{a}\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} +\mathrm{a}−\mathrm{at}^{\mathrm{2}} }=\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{1}−\mathrm{a}\right)\mathrm{t}^{\mathrm{2}} +\mathrm{1}+\mathrm{a}} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{a}−\mathrm{1}\right)\mathrm{t}^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{a}\right)}=\frac{−\mathrm{2}}{\mathrm{a}−\mathrm{1}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}−\mathrm{1}}} \\ $$$$=_{\mathrm{t}=\sqrt{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}−\mathrm{1}}}\mathrm{u}} \:\:\:\:\frac{−\mathrm{2}}{\mathrm{a}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}} \:\:\:\:\frac{\sqrt{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}−\mathrm{1}}}}{\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}−\mathrm{1}}\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)}\mathrm{du} \\ $$$$=\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}×\frac{\sqrt{\mathrm{a}+\mathrm{1}}}{\:\sqrt{\mathrm{a}−\mathrm{1}}}×\frac{−\mathrm{2}}{\mathrm{a}−\mathrm{1}}\int_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}} \:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\sqrt{\mathrm{a}−\mathrm{1}}}{\:\sqrt{\mathrm{a}+\mathrm{1}}}×\frac{−\mathrm{2}}{\mathrm{a}−\mathrm{1}}\int...\:\mathrm{du} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\int_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}} \:\:\:\left(\frac{\mathrm{1}}{\mathrm{u}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\right)\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\left[\mathrm{ln}\mid\frac{\mathrm{u}+\mathrm{1}}{\mathrm{u}−\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\left\{\mathrm{ln}\mid\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}+\mathrm{1}}{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}−\mathrm{1}}\mid\right\}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\pi}{\mathrm{4a}}\:−\frac{\mathrm{1}}{\mathrm{a}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\mathrm{ln}\mid\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}+\mathrm{1}}{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}−\mathrm{1}}\mid\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{4}}\mathrm{lna}−\int\:\:\frac{\mathrm{1}}{\mathrm{a}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\mathrm{ln}\left(\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}+\mathrm{1}}{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}}−\mathrm{1}}\right)\:+\mathrm{C} \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$
Answered by Lordose last updated on 23/Dec/21

$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{x}\right)\right)\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:+\:\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\mathrm{dx}\:\:\:\:\: \\ $$$$\Omega\:=\:\mathrm{ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{1dx}\:+\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\mathrm{dx}\:+\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\mathrm{dx}\:\:\:\:\: \\ $$$$\Omega\:=\:\frac{\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:+\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\mathrm{dx}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{1dx}\:+\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)\right)\mathrm{dx}\:\:\:\:\:\:\:\: \\ $$$$\boldsymbol{\mathrm{N}}.\boldsymbol{\mathrm{B}}\:::\:\int_{\mathrm{0}} ^{\:\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{sin}}\left(\frac{\boldsymbol{\mathrm{t}}}{\mathrm{2}}\right)\right)\boldsymbol{\mathrm{dt}}\:=\:−\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)\:−\:\boldsymbol{\mathrm{xln}}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\boldsymbol{\pi}\right)\:=\:\mathrm{0};\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2}}\right)\:=\:\boldsymbol{\mathrm{G}}\left(\boldsymbol{\mathrm{Catalan}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{Constant}}\right) \\ $$$$\Omega\:=\:\frac{\mathrm{3}\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\:+\:\mathrm{A}\:+\:\mathrm{B} \\ $$$$\mathrm{A}\:\overset{\frac{\mathrm{x}}{\mathrm{2}}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}−\frac{\mathrm{u}}{\mathrm{2}}} {=}\int_{\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}} ^{\:\boldsymbol{\pi}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{du}\:=\:\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{du}\:−\:\int_{\mathrm{0}} ^{\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{du} \\ $$$$\mathrm{A}\:=\:−\mathrm{Cl}_{\mathrm{2}} \left(\boldsymbol{\pi}\right)\:−\:\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)\:+\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}\right)\:+\:\frac{\mathrm{3}\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\mathrm{A}\:=\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}\right)\:−\:\frac{\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\mathrm{B}\:\overset{\frac{\mathrm{x}}{\mathrm{2}}\:=\:\frac{\mathrm{u}}{\mathrm{2}}−\frac{\boldsymbol{\pi}}{\mathrm{4}}} {=}\:\int_{\frac{\boldsymbol{\pi}}{\mathrm{2}}} ^{\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{du}\:=\:\int_{\mathrm{0}} ^{\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{du}\:−\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{du} \\ $$$$\mathrm{B}\:=\:−\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}\right)\:−\:\frac{\mathrm{3}\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:+\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2}}\right)\:+\:\frac{\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\mathrm{B}\:=\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2}}\right)\:−\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}\right)\:−\:\frac{\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\Omega\:=\:\frac{\mathrm{3}\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\:+\:\mathrm{A}\:+\:\mathrm{B} \\ $$$$\Omega\:=\:\frac{\mathrm{3}\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\:+\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}\right)\:−\:\frac{\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\:+\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2}}\right)−\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}\right)\:−\:\frac{\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\Omega\:=\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{2}}\right)\:−\:\frac{\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$\boldsymbol{\Omega}\:=\:\boldsymbol{\mathrm{G}}\:−\:\frac{\boldsymbol{\pi\mathrm{log}}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$
