
Question Number 222512 by Shrodinger last updated on 28/Jun/25
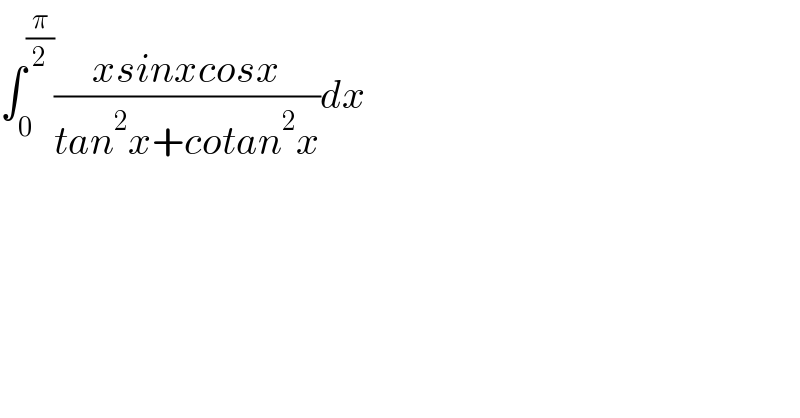
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{xsinxcosx}}{{tan}^{\mathrm{2}} {x}+{cotan}^{\mathrm{2}} {x}}{dx} \\ $$
Answered by mr W last updated on 29/Jun/25
![I=∫_0 ^(π/2) ((x sin x cos x)/(tan^2 t+cot^2 x))dx say x=(π/2)−t I=−∫_(π/2) ^0 ((((π/2)−t)cos t sin t)/(cot^2 t+tan^2 t))dt =∫_0 ^(π/2) ((((π/2)−t)cos t sin t)/(cot^2 t+tan^2 t))dt =(π/2)∫_0 ^(π/2) ((cos t sin t)/(cot^2 t+tan^2 t))dt−∫_0 ^(π/2) ((t cos t sin t)/(cot^2 t+tan^2 t))dt =(π/2)∫_0 ^(π/2) ((cos t sin t)/(cot^2 t+tan^2 t))dt−I I=(π/4)∫_0 ^(π/2) ((cos t sin t)/(cot^2 t+tan^2 t))dt =(π/4)∫_0 ^(π/2) ((sin^3 t cos^3 t)/( sin^4 t+cos^4 t))dt =(π/4)∫_0 ^(π/2) ((sin^3 t cos^3 t)/( 1−2 sin^2 t cos^2 t))dt =(π/(16))∫_0 ^(π/2) ((8 sin^3 t cos^3 t)/( 2−4 sin^2 t cos^2 t))dt =(π/(16))∫_0 ^(π/2) ((sin^3 2t)/( 2−sin^2 2t))dt =(π/(32))∫_0 ^π ((sin^3 x)/( 2−sin^2 x))dx =(π/(32))∫_0 ^π ((1−cos^2 x)/( 1+cos^2 x))d(−cos x) =(π/(32))∫_π ^0 ((1−cos^2 x)/( 1+cos^2 x))d(cos x) =(π/(32))∫_(−1) ^1 ((1−u^2 )/( 1+u^2 ))du =(π/(32))∫_(−1) ^1 ((2/( 1+u^2 ))−1)du =(π/(32))(2∫_(−1) ^1 (du/( 1+u^2 ))−2) =(π/(32))(4∫_0 ^1 (du/( 1+u^2 ))−2) =(π/(32))(4[tan^(−1) u]_0 ^1 −2) =(π/(32))(4×(π/4)−2) =((π(π−2))/(32))≈0.112076 ✓](Q222514.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{tan}^{\mathrm{2}} \:{t}+\mathrm{cot}^{\mathrm{2}} \:{x}}{dx} \\ $$$${say}\:{x}=\frac{\pi}{\mathrm{2}}−{t} \\ $$$${I}=−\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{\left(\frac{\pi}{\mathrm{2}}−{t}\right)\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}}{\mathrm{cot}^{\mathrm{2}} \:{t}+\mathrm{tan}^{\mathrm{2}} \:{t}}{dt} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\frac{\pi}{\mathrm{2}}−{t}\right)\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}}{\mathrm{cot}^{\mathrm{2}} \:{t}+\mathrm{tan}^{\mathrm{2}} \:{t}}{dt} \\ $$$$\:\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}}{\mathrm{cot}^{\mathrm{2}} \:{t}+\mathrm{tan}^{\mathrm{2}} \:{t}}{dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{t}\:\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}}{\mathrm{cot}^{\mathrm{2}} \:{t}+\mathrm{tan}^{\mathrm{2}} \:{t}}{dt} \\ $$$$\:\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}}{\mathrm{cot}^{\mathrm{2}} \:{t}+\mathrm{tan}^{\mathrm{2}} \:{t}}{dt}−{I} \\ $$$${I}=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}}{\mathrm{cot}^{\mathrm{2}} \:{t}+\mathrm{tan}^{\mathrm{2}} \:{t}}{dt} \\ $$$$\:\:=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{3}} \:{t}\:\mathrm{cos}^{\mathrm{3}} \:{t}}{\:\mathrm{sin}^{\mathrm{4}} \:{t}+\mathrm{cos}^{\mathrm{4}} \:{t}}{dt} \\ $$$$\:\:=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{3}} \:{t}\:\mathrm{cos}^{\mathrm{3}} \:{t}}{\:\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{t}\:\mathrm{cos}^{\mathrm{2}} \:{t}}{dt} \\ $$$$\:\:=\frac{\pi}{\mathrm{16}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{8}\:\mathrm{sin}^{\mathrm{3}} \:{t}\:\mathrm{cos}^{\mathrm{3}} \:{t}}{\:\mathrm{2}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{t}\:\mathrm{cos}^{\mathrm{2}} \:{t}}{dt} \\ $$$$\:\:=\frac{\pi}{\mathrm{16}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{3}} \:\mathrm{2}{t}}{\:\mathrm{2}−\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{t}}{dt} \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sin}^{\mathrm{3}} \:{x}}{\:\mathrm{2}−\mathrm{sin}^{\mathrm{2}} \:{x}}{dx} \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}}{\:\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}{d}\left(−\mathrm{cos}\:{x}\right) \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\int_{\pi} ^{\mathrm{0}} \frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}}{\:\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}{d}\left(\mathrm{cos}\:{x}\right) \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}−{u}^{\mathrm{2}} }{\:\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\int_{−\mathrm{1}} ^{\mathrm{1}} \left(\frac{\mathrm{2}}{\:\mathrm{1}+{u}^{\mathrm{2}} }−\mathrm{1}\right){du} \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\left(\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{du}}{\:\mathrm{1}+{u}^{\mathrm{2}} }−\mathrm{2}\right) \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\left(\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{\:\mathrm{1}+{u}^{\mathrm{2}} }−\mathrm{2}\right) \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\left(\mathrm{4}\left[\mathrm{tan}^{−\mathrm{1}} {u}\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\right) \\ $$$$\:\:=\frac{\pi}{\mathrm{32}}\left(\mathrm{4}×\frac{\pi}{\mathrm{4}}−\mathrm{2}\right) \\ $$$$\:\:=\frac{\pi\left(\pi−\mathrm{2}\right)}{\mathrm{32}}\approx\mathrm{0}.\mathrm{112076}\:\checkmark \\ $$
Commented by Shrodinger last updated on 29/Jun/25

$${Thanks}\:{Sir} \\ $$
Commented by mnjuly1970 last updated on 29/Jun/25

$$\: \\ $$
