
Question Number 208692 by Ghisom last updated on 21/Jun/24
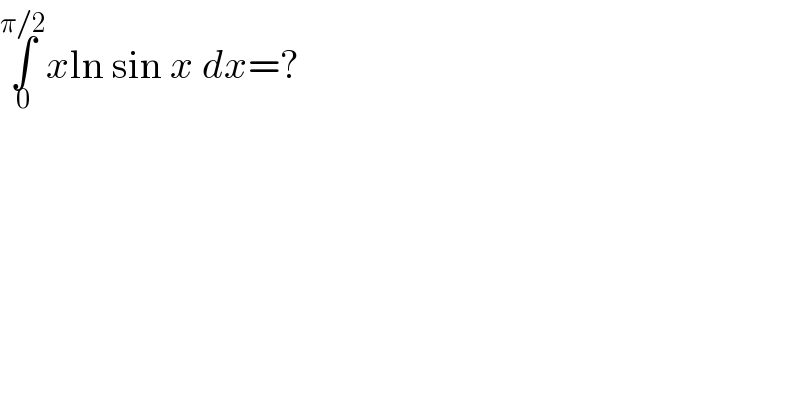
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}{x}\mathrm{ln}\:\mathrm{sin}\:{x}\:{dx}=? \\ $$
Answered by Berbere last updated on 21/Jun/24
![ln(sin(x))=−ln(2)−Σ_(k≥1) ((cos(2kx))/k) proof ln(sin(x))=Re(ln(sin(x)) ln(sin(x)=ln(((e^(ix) −e^(−ix) )/(2i))) ln(sin(x))=ln(e^(ix) (1−e^(−2ix) ))−ln(2)==ix−ln(2)−Σ(e^(−2kix) /k) Reln(sin(x))=−ln(2)−Σ((cos(2kx))/k) ∫_0 ^(π/2) xln(sin(x))dx=∫_0 ^(π/2) x(−ln(2)−Σ((cos(2kx))/k)) =[−(x^2 /2)ln(2)]_0 ^(π/2) −Σ_(k≥1) (1/k)∫_0 ^(π/2) xcos(2kx)dx^� ∫xcos(2kx)dx=x.((sin(2kx))/(2k))+((cos(2kx))/(4k^2 )) .−(π^2 /8)ln(2)−Σ_k (1/k)[((sin(2kx))/(2k))+((cos(2kx))/(4k^2 ))]_0 ^(π/2) =−(π^2 /8)ln(2)−Σ(((−1)^k −1)/(4k^3 )) =−(π^3 /8)ln(2)+Σ_(k≥0) (1/(2(2k+1)^3 ))=−(π^3 /8)ln(2)+(7/(16))ζ(3)](Q208694.png)
$${ln}\left({sin}\left({x}\right)\right)=−{ln}\left(\mathrm{2}\right)−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}{kx}\right)}{{k}} \\ $$$${proof}\:{ln}\left({sin}\left({x}\right)\right)={Re}\left({ln}\left({sin}\left({x}\right)\right)\right. \\ $$$${ln}\left({sin}\left({x}\right)={ln}\left(\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}}\right)\right. \\ $$$${ln}\left({sin}\left({x}\right)\right)={ln}\left({e}^{{ix}} \left(\mathrm{1}−{e}^{−\mathrm{2}{ix}} \right)\right)−{ln}\left(\mathrm{2}\right)=={ix}−{ln}\left(\mathrm{2}\right)−\Sigma\frac{{e}^{−\mathrm{2}{kix}} }{{k}} \\ $$$${Reln}\left({sin}\left({x}\right)\right)=−{ln}\left(\mathrm{2}\right)−\Sigma\frac{{cos}\left(\mathrm{2}{kx}\right)}{{k}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xln}\left({sin}\left({x}\right)\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}\left(−{ln}\left(\mathrm{2}\right)−\Sigma\frac{{cos}\left(\mathrm{2}{kx}\right)}{{k}}\right) \\ $$$$=\left[−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{ln}\left(\mathrm{2}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{k}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xcos}\left(\mathrm{2}{kx}\right){d}\bar {{x}} \\ $$$$\int{xcos}\left(\mathrm{2}{kx}\right){dx}={x}.\frac{{sin}\left(\mathrm{2}{kx}\right)}{\mathrm{2}{k}}+\frac{{cos}\left(\mathrm{2}{kx}\right)}{\mathrm{4}{k}^{\mathrm{2}} } \\ $$$$.−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}{ln}\left(\mathrm{2}\right)−\underset{{k}} {\sum}\frac{\mathrm{1}}{{k}}\left[\frac{{sin}\left(\mathrm{2}{kx}\right)}{\mathrm{2}{k}}+\frac{{cos}\left(\mathrm{2}{kx}\right)}{\mathrm{4}{k}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}{ln}\left(\mathrm{2}\right)−\Sigma\frac{\left(−\mathrm{1}\right)^{{k}} −\mathrm{1}}{\mathrm{4}{k}^{\mathrm{3}} } \\ $$$$=−\frac{\pi^{\mathrm{3}} }{\mathrm{8}}{ln}\left(\mathrm{2}\right)+\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{3}} }=−\frac{\pi^{\mathrm{3}} }{\mathrm{8}}{ln}\left(\mathrm{2}\right)+\frac{\mathrm{7}}{\mathrm{16}}\zeta\left(\mathrm{3}\right) \\ $$
Commented by Ghisom last updated on 22/Jun/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
