
Question Number 69328 by mhmd last updated on 22/Sep/19
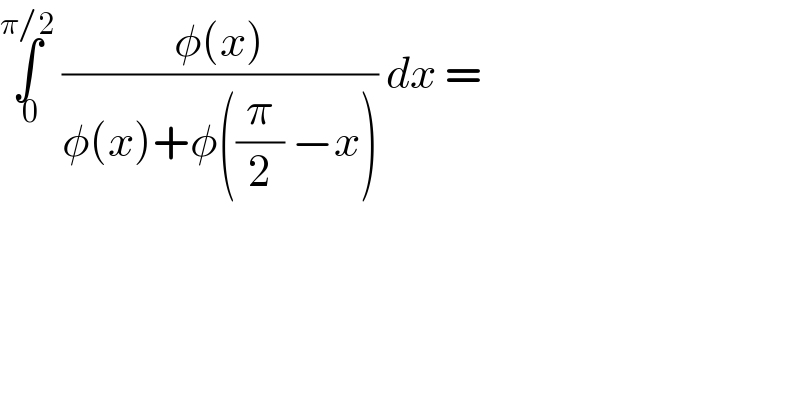
$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\phi\left({x}\right)}{\phi\left({x}\right)+\phi\left(\frac{\pi}{\mathrm{2}}\:−{x}\right)}\:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 22/Sep/19
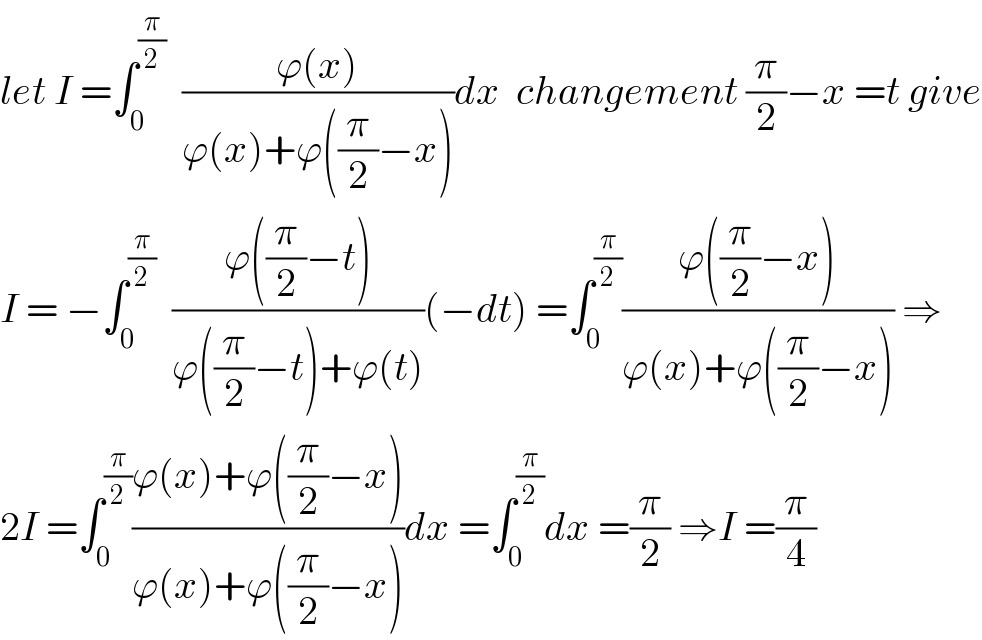
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\varphi\left({x}\right)}{\varphi\left({x}\right)+\varphi\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx}\:\:{changement}\:\frac{\pi}{\mathrm{2}}−{x}\:={t}\:{give} \\ $$$${I}\:=\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\varphi\left(\frac{\pi}{\mathrm{2}}−{t}\right)}{\varphi\left(\frac{\pi}{\mathrm{2}}−{t}\right)+\varphi\left({t}\right)}\left(−{dt}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\varphi\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{\varphi\left({x}\right)+\varphi\left(\frac{\pi}{\mathrm{2}}−{x}\right)}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\varphi\left({x}\right)+\varphi\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{\varphi\left({x}\right)+\varphi\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow{I}\:=\frac{\pi}{\mathrm{4}} \\ $$
