
Question Number 89052 by M±th+et£s last updated on 15/Apr/20
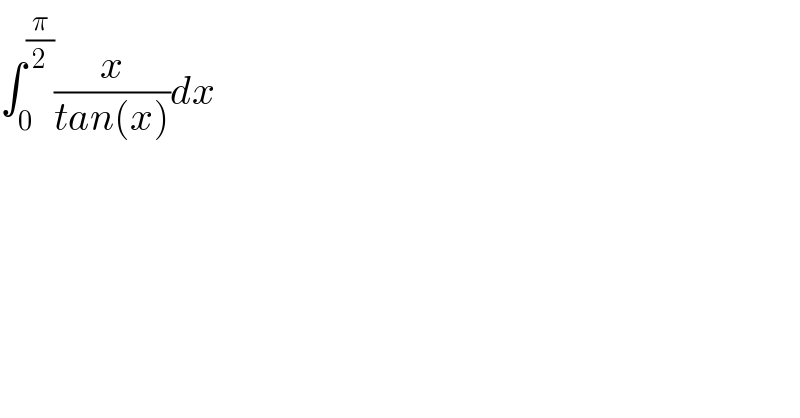
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}}{{tan}\left({x}\right)}{dx} \\ $$
Commented by abdomathmax last updated on 15/Apr/20
![I =∫_0 ^(π/2) (x/(tanx))dx ⇒I =_(tanx=t) ∫_0 ^∞ ((arctan(t))/t)(dt/(1+t^2 )) =∫_0 ^∞ ((arctan(t))/(t(1+t^2 )))dt let f(a) =∫_0 ^∞ ((arctan(at))/(t(1+t^2 )))dt f^′ (a) =∫_0 ^∞ (dt/((1+a^2 t^2 )(1+t^2 ))) =_(at=u) ∫_0 ^∞ (du/(a(1+u^2 )(1+(u^2 /a^2 ))))(du/a) =∫_0 ^∞ (du/((1+u^2 )(a^2 +u^2 ))) decomposition of F(u) =(1/((u^2 +1)(u^2 +a^2 ))) =((αu +β)/(u^2 +1)) +((λu +ρ)/(u^2 +a^2 )) F(−u)=F(u) ⇒ ((−αu +β)/(u^2 +1)) +((−λu +ρ)/(u^2 +a^2 )) =F(u) ⇒α=λ=0 and ρ=β ⇒ F(u)=(β/(u^2 +1)) +(ρ/(u^2 +a^2 )) lim_(u→+∞) u^2 F(u) =0 =β+ρ ⇒ρ=−β ⇒ F(u)=(β/(u^2 +1))−(β/(u^2 +a^2 )) F(0)=(1/a^2 ) =β−(β/a^2 ) ⇒1 =a^2 β−β =(a^2 −1)β ⇒ β =(1/(a^2 −1)) ⇒F(u)=(1/(a^2 −1))((1/(u^2 +1))−(1/(u^2 +a^2 ))) ⇒ f^′ (a)=(1/(a^2 −1))∫_0 ^∞ ((1/(u^2 +1))−(1/(u^2 +a^2 )))du ∫ (du/(u^2 +a^2 )) =_(u=az) ∫ ((adz)/(a^2 (1+z^2 ))) =(1/a) arctan((u/a)) ⇒ f^′ (a) =(1/(a^2 −1))[arctanu −(1/a)arctan((u/a))]_0 ^(+∞) =(1/(a^2 −1)){(π/2)−(π/(2a))} =(π/2)×(1/(a^2 −1))(1−(1/a)) =(π/(2(a^2 −1)))(((a−1)/a)) =(π/(2a(a+1))) ⇒ f(a) =(π/2) ∫ (da/(a(a+1))) +c =(π/2)∫((1/a)−(1/(a+1)))da +c =(π/2)ln∣(a/(a+1))∣ +c c =lim_(a→+∞) f(a) I =f(1) =(π/2)ln((1/2)) +c =c−(π/2)ln(2) rest to find c...](Q89057.png)
$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{{tanx}}{dx}\:\Rightarrow{I}\:=_{{tanx}={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({t}\right)}{{t}}\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({t}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}\:\:{let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left({at}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left(\mathrm{1}+{a}^{\mathrm{2}} {t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$=_{{at}={u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{du}}{{a}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{{u}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}\frac{{du}}{{a}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} \:+{u}^{\mathrm{2}} \right)}\:{decomposition}\:{of} \\ $$$${F}\left({u}\right)\:=\frac{\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)}\:=\frac{\alpha{u}\:+\beta}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\lambda{u}\:+\rho}{{u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$$${F}\left(−{u}\right)={F}\left({u}\right)\:\Rightarrow \\ $$$$\frac{−\alpha{u}\:+\beta}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−\lambda{u}\:+\rho}{{u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:={F}\left({u}\right)\:\Rightarrow\alpha=\lambda=\mathrm{0}\:{and}\:\rho=\beta\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{\beta}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\rho}{{u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow+\infty} \:{u}^{\mathrm{2}} \:{F}\left({u}\right)\:=\mathrm{0}\:=\beta+\rho\:\Rightarrow\rho=−\beta\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{\beta}{{u}^{\mathrm{2}} +\mathrm{1}}−\frac{\beta}{{u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:=\beta−\frac{\beta}{{a}^{\mathrm{2}} }\:\Rightarrow\mathrm{1}\:={a}^{\mathrm{2}} \beta−\beta\:=\left({a}^{\mathrm{2}} −\mathrm{1}\right)\beta\:\Rightarrow \\ $$$$\beta\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow{F}\left({u}\right)=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\right){du} \\ $$$$\int\:\frac{{du}}{{u}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:=_{{u}={az}} \:\:\int\:\frac{{adz}}{{a}^{\mathrm{2}} \left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{{a}}\:{arctan}\left(\frac{{u}}{{a}}\right)\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\left[{arctanu}\:−\frac{\mathrm{1}}{{a}}{arctan}\left(\frac{{u}}{{a}}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\left\{\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}{a}}\right\}\:=\frac{\pi}{\mathrm{2}}×\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{1}\right)}\left(\frac{{a}−\mathrm{1}}{{a}}\right)\:=\frac{\pi}{\mathrm{2}{a}\left({a}+\mathrm{1}\right)}\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}\:\int\:\:\frac{{da}}{{a}\left({a}+\mathrm{1}\right)}\:+{c} \\ $$$$=\frac{\pi}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{a}+\mathrm{1}}\right){da}\:+{c}\:=\frac{\pi}{\mathrm{2}}{ln}\mid\frac{{a}}{{a}+\mathrm{1}}\mid\:+{c} \\ $$$${c}\:\:={lim}_{{a}\rightarrow+\infty} \:\:{f}\left({a}\right) \\ $$$${I}\:={f}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:+{c}\:={c}−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$$${rest}\:{to}\:{find}\:{c}... \\ $$$$ \\ $$$$ \\ $$
Commented by abdomathmax last updated on 15/Apr/20

$${let}\:{try}\:\:{residus}\:{method}\:\:{we}?{hsve} \\ $$$${I}?=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({t}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dx}\Rightarrow\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({t}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$ \\ $$$${let}\:\varphi\left({z}\right)=\frac{{arctan}\left({z}\right)}{{z}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:\Rightarrow\varphi\left({z}\right)\:=\frac{{arctanz}}{{z}\left({z}−{i}\right)\left({z}+{i}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{{Res}\left(\varphi,{i}\right)\:+{Res}\left(\varphi,{o}\right)\right\} \\ $$$$=\mathrm{2}{i}\pi×\frac{{arctan}\left({i}\right)}{{i}\left(\mathrm{2}{i}\right)}\:=−{i}\pi\:{arctan}\left({i}\right) \\ $$$${but}\:{the}\:{frmula}\:\:{arctan}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right)\:{is}\:{not} \\ $$$${valide}\:{for}\:{z}={i}...{be}\:{continued}... \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 15/Apr/20

$${thanx}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 15/Apr/20

$${you}\:{are}\:{welcome} \\ $$
