
Question Number 157412 by cortano last updated on 23/Oct/21
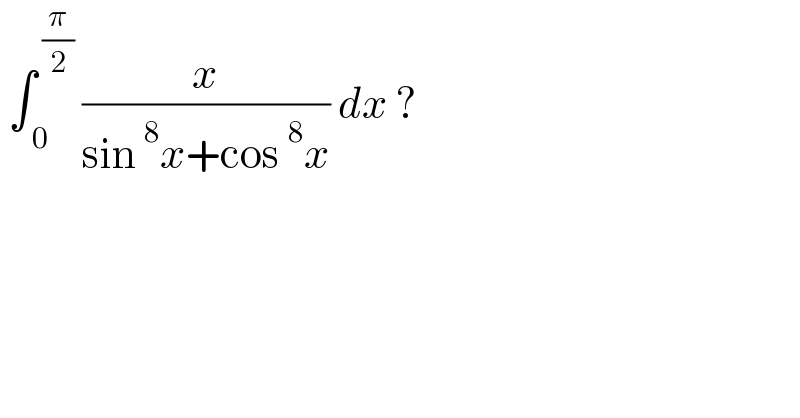
$$\:\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{\mathrm{sin}\:^{\mathrm{8}} {x}+\mathrm{cos}\:^{\mathrm{8}} {x}}\:{dx}\:? \\ $$
Answered by phanphuoc last updated on 23/Oct/21
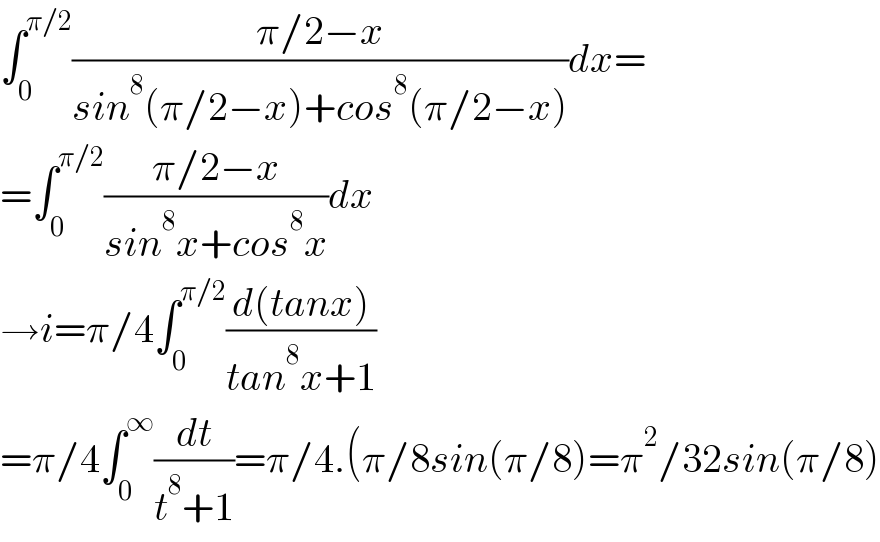
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\pi/\mathrm{2}−{x}}{{sin}^{\mathrm{8}} \left(\pi/\mathrm{2}−{x}\right)+{cos}^{\mathrm{8}} \left(\pi/\mathrm{2}−{x}\right)}{dx}= \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\pi/\mathrm{2}−{x}}{{sin}^{\mathrm{8}} {x}+{cos}^{\mathrm{8}} {x}}{dx} \\ $$$$\rightarrow{i}=\pi/\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{d}\left({tanx}\right)}{{tan}^{\mathrm{8}} {x}+\mathrm{1}} \\ $$$$=\pi/\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{8}} +\mathrm{1}}=\pi/\mathrm{4}.\left(\pi/\mathrm{8}{sin}\left(\pi/\mathrm{8}\right)=\pi^{\mathrm{2}} /\mathrm{32}{sin}\left(\pi/\mathrm{8}\right)\right. \\ $$
Commented by cortano last updated on 23/Oct/21
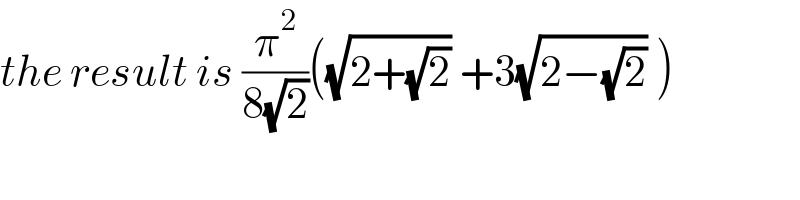
$${the}\:{result}\:{is}\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}\sqrt{\mathrm{2}}}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\:+\mathrm{3}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\:\right) \\ $$
Answered by phanphuoc last updated on 23/Oct/21
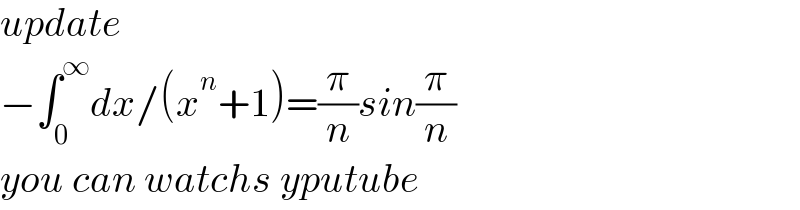
$${update} \\ $$$$−\int_{\mathrm{0}} ^{\infty} {dx}/\left({x}^{{n}} +\mathrm{1}\right)=\frac{\pi}{{n}}{sin}\frac{\pi}{{n}} \\ $$$${you}\:{can}\:{watchs}\:{yputube} \\ $$
