
Question Number 137197 by Fikret last updated on 30/Mar/21
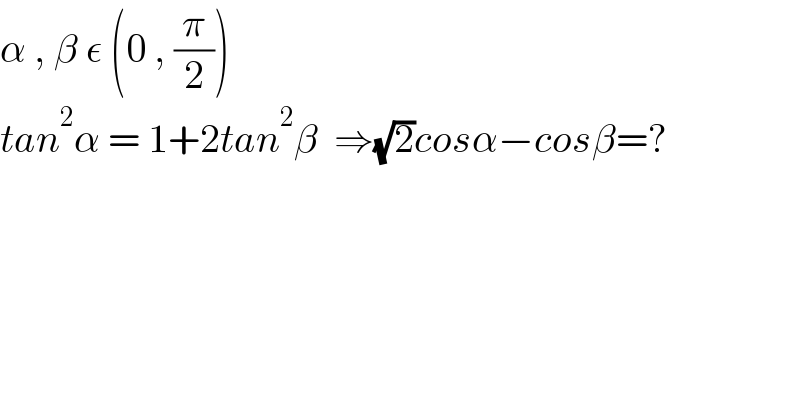
$$\alpha\:,\:\beta\:\epsilon\:\left(\mathrm{0}\:,\:\frac{\pi}{\mathrm{2}}\right) \\ $$$${tan}^{\mathrm{2}} \alpha\:=\:\mathrm{1}+\mathrm{2}{tan}^{\mathrm{2}} \beta\:\:\Rightarrow\sqrt{\mathrm{2}}{cos}\alpha−{cos}\beta=? \\ $$
Answered by MJS_new last updated on 31/Mar/21
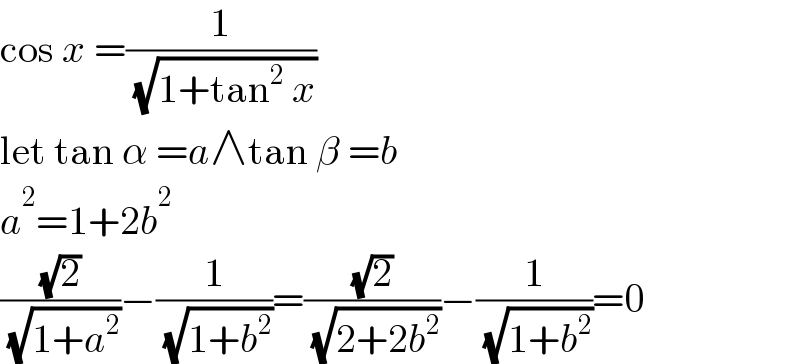
$$\mathrm{cos}\:{x}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}}} \\ $$$$\mathrm{let}\:\mathrm{tan}\:\alpha\:={a}\wedge\mathrm{tan}\:\beta\:={b} \\ $$$${a}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{b}^{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{b}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}+\mathrm{2}{b}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{b}^{\mathrm{2}} }}=\mathrm{0} \\ $$
