
Question Number 181643 by Frix last updated on 28/Nov/22
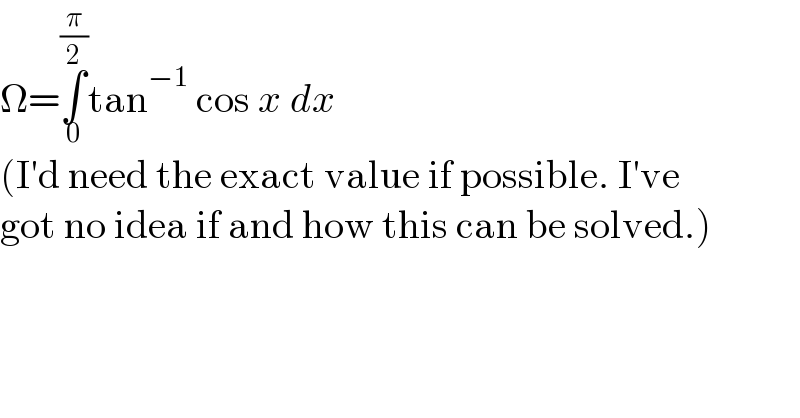
$$\Omega=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{tan}^{−\mathrm{1}} \:\mathrm{cos}\:{x}\:{dx} \\ $$$$\left(\mathrm{I}'\mathrm{d}\:\mathrm{need}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{if}\:\mathrm{possible}.\:\mathrm{I}'\mathrm{ve}\right. \\ $$$$\left.\mathrm{got}\:\mathrm{no}\:\mathrm{idea}\:\mathrm{if}\:\mathrm{and}\:\mathrm{how}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}.\right) \\ $$
Commented by MJS_new last updated on 28/Nov/22
![it′s possible to solve the integral but it′s very complicated and I don′t think you could use the exact value. Ω≈.845291 www.wolframalpha.com gives the exact indefinite integral which needs about 25 lines but only an approximate value for [0; π/2]](Q181650.png)
$$\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{very} \\ $$$$\mathrm{complicated}\:\mathrm{and}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{you}\:\mathrm{could}\:\mathrm{use} \\ $$$$\mathrm{the}\:\mathrm{exact}\:\mathrm{value}. \\ $$$$\Omega\approx.\mathrm{845291} \\ $$$$\mathrm{www}.\mathrm{wolframalpha}.\mathrm{com}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{exact} \\ $$$$\mathrm{indefinite}\:\mathrm{integral}\:\mathrm{which}\:\mathrm{needs}\:\mathrm{about}\:\mathrm{25} \\ $$$$\mathrm{lines}\:\mathrm{but}\:\mathrm{only}\:\mathrm{an}\:\mathrm{approximate}\:\mathrm{value}\:\mathrm{for}\:\left[\mathrm{0};\:\pi/\mathrm{2}\right] \\ $$
Commented by Frix last updated on 28/Nov/22

$$\mathrm{Ok}\:\mathrm{I}\:\mathrm{see}... \\ $$
