
Question Number 52900 by MJS last updated on 15/Jan/19
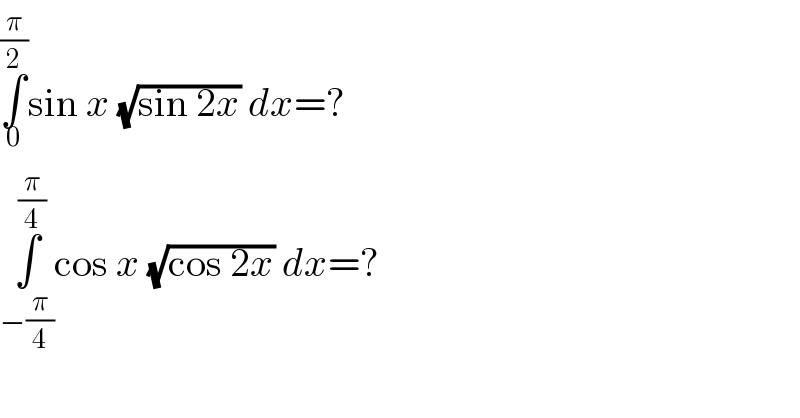
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{sin}\:{x}\:\sqrt{\mathrm{sin}\:\mathrm{2}{x}}\:{dx}=? \\ $$$$\underset{−\frac{\pi}{\mathrm{4}}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:{dx}=? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
![I=∫_0 ^(π/2) sinx(√(sin2x)) dx I=∫_0 ^(π/2) cosx(√(sin2x)) dx [∫_0 ^a f(x)dx=∫_0 ^a f(a−x)dx] 2I=∫_0 ^(π/2) (cosx+sinx)(√(sin2x)) dx =∫_0 ^(π/2) d(sinx−cosx)(√(1−(1−sin2x))) dx ∫_0 ^(π/2) d(sinx−cosx)(√(1−(sinx−cosx)^2 )) dx ∣(((sinx−cosx)(√(1−(sinx−cosx)^2 )))/2)+(1/2)sin^(−1) (((sinx−cosx)/1))∣_0 ^(π/2) =[{(((1−0)(√(1−(1−0)^2 )))/2)+(1/2)sin^(−1) (((1−0)/1))}−{((0−1(√(1−1)))/2)+(1/2)sin^(−1) (((0−1)/1))}] =(1/2)×(π/2)−{(1/2)×(((−π)/2))} =(π/4)+(π/4)=(π/2) so I=(1/2)×(π/2)=(π/4) sir pls check...](Q52916.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sinx}\sqrt{{sin}\mathrm{2}{x}}\:{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosx}\sqrt{{sin}\mathrm{2}{x}}\:{dx}\:\:\left[\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{{a}} {f}\left({a}−{x}\right){dx}\right] \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cosx}+{sinx}\right)\sqrt{{sin}\mathrm{2}{x}}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {d}\left({sinx}−{cosx}\right)\sqrt{\mathrm{1}−\left(\mathrm{1}−{sin}\mathrm{2}{x}\right)}\:{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {d}\left({sinx}−{cosx}\right)\sqrt{\mathrm{1}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\mid\frac{\left({sinx}−{cosx}\right)\sqrt{\mathrm{1}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{sinx}−{cosx}}{\mathrm{1}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\left[\left\{\frac{\left(\mathrm{1}−\mathrm{0}\right)\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{0}\right)^{\mathrm{2}} }}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{1}}\right)\right\}−\left\{\frac{\mathrm{0}−\mathrm{1}\sqrt{\mathrm{1}−\mathrm{1}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{0}−\mathrm{1}}{\mathrm{1}}\right)\right\}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}−\left\{\frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{−\pi}{\mathrm{2}}\right)\right\} \\ $$$$=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}\:\:{sir}\:{pls}\:{check}... \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
![∫_(−(π/4)) ^(π/4) cosx(√(cos2x)) dx ∫_(−a) ^a f(x)dx=2×∫_0 ^a f(x)dx [here f(x)=evenfunction] so∫_((−π)/4) ^(π/4) cosx(√(cos2x)) dx=2×∫_0 ^(π/4) cosx(√(cos2x)) dx now using help of graph...](Q52919.png)
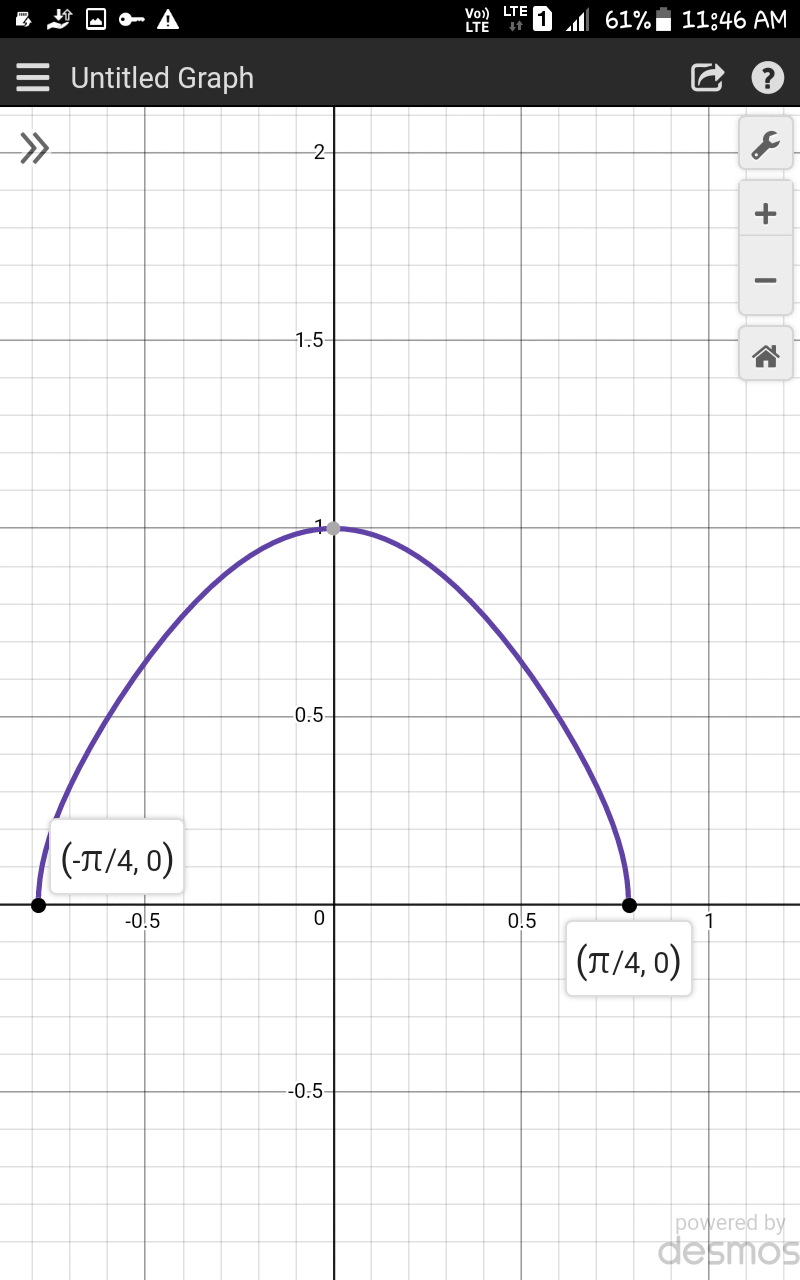
$$\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:{cosx}\sqrt{{cos}\mathrm{2}{x}}\:{dx} \\ $$$$ \\ $$$$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}=\mathrm{2}×\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}\:\left[{here}\:{f}\left({x}\right)={evenfunction}\right] \\ $$$${so}\int_{\frac{−\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:{cosx}\sqrt{{cos}\mathrm{2}{x}}\:{dx}=\mathrm{2}×\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cosx}\sqrt{{cos}\mathrm{2}{x}}\:{dx} \\ $$$${now}\:{using}\:{help}\:{of}\:{graph}... \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19

$${so}\:\int_{\frac{−\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:{cosx}\sqrt{{cos}\mathrm{2}{x}}\:{dx}={area}\:{under}\:{the}\:{curve} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\frac{\mathrm{2}}{\mathrm{3}}×\frac{\pi}{\mathrm{2}}×\mathrm{1}=\frac{\pi}{\mathrm{3}} \\ $$$${roughly}\:{it}\:{is}\:{a}\:{parabola}\:{sir}...{so}\:{area} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{ab} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19

Answered by mr W last updated on 16/Jan/19
![∫_(−(π/4)) ^(π/4) cos x (√(cos 2x)) dx =2∫_0 ^(π/4) cos x (√(cos 2x)) dx =2∫_0 ^(π/4) cos x(√(1−2 sin^2 x)) dx =(√2)∫_0 ^(π/4) (√(1−((√2) sin x)^2 )) d((√2) sin x) (∫(√(1−t^2 )) dt) =((√2)/2)[sin^(−1) ((√2) sin x)+((√2) sin x)(√(1−((√2) sin x)^2 ))]_0 ^(π/4) =((√2)/2)((π/2)) =((π(√2))/4)](Q52990.png)
$$\underset{−\frac{\pi}{\mathrm{4}}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:{dx} \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:\mathrm{2}{x}}\:{dx} \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\mathrm{cos}\:{x}\sqrt{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{x}}\:{dx} \\ $$$$=\sqrt{\mathrm{2}}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{4}}} {\int}}\sqrt{\mathrm{1}−\left(\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\:{d}\left(\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\right)\:\:\:\:\:\:\:\:\left(\int\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left[\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\right)+\left(\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\right)\sqrt{\mathrm{1}−\left(\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
