
Question Number 156028 by mnjuly1970 last updated on 07/Oct/21
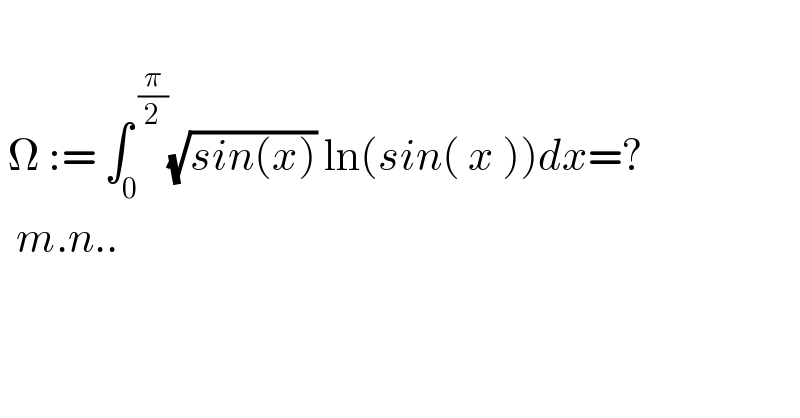
$$ \\ $$$$\:\Omega\::=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \sqrt{{sin}\left({x}\right)}\:\mathrm{ln}\left({sin}\left(\:{x}\:\right)\right){dx}=? \\ $$$$\:\:{m}.{n}.. \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 07/Oct/21
![f(α)=∫_0 ^(π/2) sin^α xdx=(1/2)β(((α+1)/2), (1/2))=((Γ(((α+1)/2))(√π))/(2Γ((α/2)+1))) f ′(α)=∫_0 ^(π/2) sin^α xln(sinx)dx=((√π)/2){((Γ((α/2)+1)Γ′(((α+1)/2))−Γ(((α+1)/2))Γ′((α/2)+1))/(Γ^2 ((α/2)+1)))} f ′((1/2))=∫_0 ^(π/2) (√(sinx))ln(sinx)dx=((√π)/2){((Γ((5/4))Γ′((3/4))−Γ((3/4))Γ′((5/4)))/(Γ^2 ((5/4))))} =((√π)/2){(((1/4)Γ((1/4))Γ((3/4))[ψ((3/4))−ψ((5/4))])/((1/(16))Γ^2 ((1/4))))} ...](Q156030.png)
$${f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\alpha} {xdx}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\sqrt{\pi}}{\mathrm{2}\Gamma\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$${f}\:'\left(\alpha\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\alpha} {x}\mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\left\{\frac{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)\Gamma'\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)−\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\Gamma'\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)}{\Gamma^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)}\right\} \\ $$$${f}\:'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{sin}{x}}\mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\left\{\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\Gamma'\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\Gamma'\left(\frac{\mathrm{5}}{\mathrm{4}}\right)}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{5}}{\mathrm{4}}\right)}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\pi}}{\mathrm{2}}\left\{\frac{\frac{\mathrm{1}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\left[\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\right]}{\frac{\mathrm{1}}{\mathrm{16}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}\right\} \\ $$$$... \\ $$
Commented by Ar Brandon last updated on 07/Oct/21
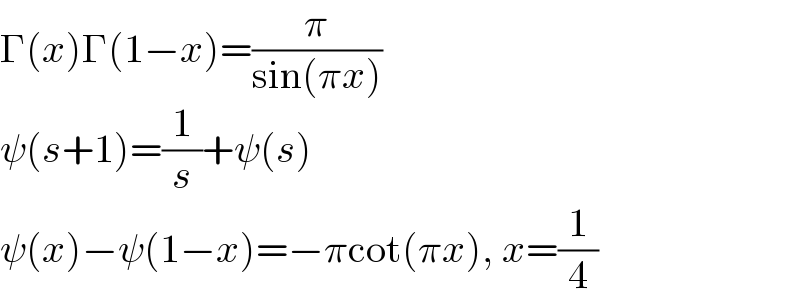
$$\Gamma\left({x}\right)\Gamma\left(\mathrm{1}−{x}\right)=\frac{\pi}{\mathrm{sin}\left(\pi{x}\right)} \\ $$$$\psi\left({s}+\mathrm{1}\right)=\frac{\mathrm{1}}{{s}}+\psi\left({s}\right) \\ $$$$\psi\left({x}\right)−\psi\left(\mathrm{1}−{x}\right)=−\pi\mathrm{cot}\left(\pi{x}\right),\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 07/Oct/21
$${grateful}\:{mr}\:{brandon}.. \\ $$
