
Question Number 220770 by mnjuly1970 last updated on 18/May/25
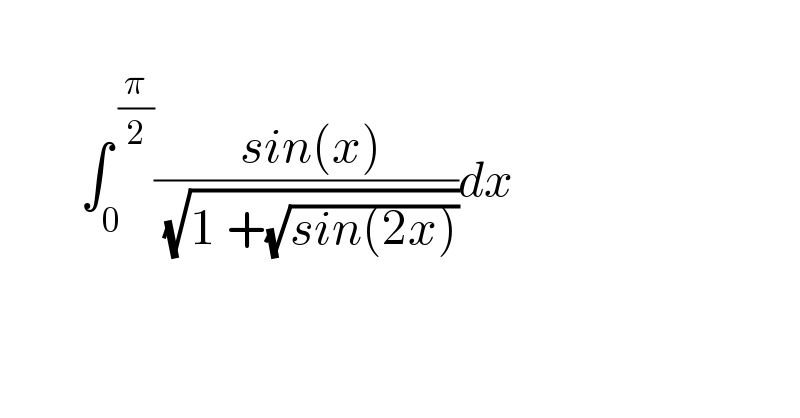
$$ \\ $$$$\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\:{sin}\left({x}\right)}{\:\sqrt{\mathrm{1}\:+\sqrt{{sin}\left(\mathrm{2}{x}\right)}}}{dx}\: \\ $$
Answered by Ghisom last updated on 21/May/25
![F(x)=∫_0 ^(π/2) ((sin x)/( (√(1+(√(sin 2x))))))dx F((π/2)−x)=−F(x) ⇒ F(x)=(1/2)(F(x)+F((π/2)−x))= =(1/2)∫_0 ^(π/2) ((cos x +sin x)/( (√(1+(√(sin 2x))))))dx= [t=x+(π/4)] =((√2)/2) ∫_(π/4) ^(3π/4) ((sin t)/( (√(1+(√(−cos 2t))))))dt= =((√2)/2) ∫_(π/4) ^(3π/4) ((sin t)/( (√(1+(√(1−2cos^2 t))))))dt= [u=(√2)cos t] =((√2)/2)∫_(−1) ^1 (du/( (√(1−u))+(√(1+u))))= =((√2)/4)∫_(−1) ^1 (((√(1+u))/u)−((√(1−u))/u))du= ((√2)/2)[ln ∣((1−(√(1+u)))/(1−(√(1−u))))∣ +(√(1+u))−(√(1−u))]_(−1) ^1 = =2−(√2)ln (1+(√2))](Q220776.png)
$${F}\left({x}\right)=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{1}+\sqrt{\mathrm{sin}\:\mathrm{2}{x}}}}{dx} \\ $$$${F}\left(\frac{\pi}{\mathrm{2}}−{x}\right)=−{F}\left({x}\right)\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({F}\left({x}\right)+{F}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{1}+\sqrt{\mathrm{sin}\:\mathrm{2}{x}}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\frac{\pi}{\mathrm{4}}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\underset{\pi/\mathrm{4}} {\overset{\mathrm{3}\pi/\mathrm{4}} {\int}}\frac{\mathrm{sin}\:{t}}{\:\sqrt{\mathrm{1}+\sqrt{−\mathrm{cos}\:\mathrm{2}{t}}}}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\underset{\pi/\mathrm{4}} {\overset{\mathrm{3}\pi/\mathrm{4}} {\int}}\frac{\mathrm{sin}\:{t}}{\:\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} \:{t}}}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{\mathrm{2}}\mathrm{cos}\:{t}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\frac{{du}}{\:\sqrt{\mathrm{1}−{u}}+\sqrt{\mathrm{1}+{u}}}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\left(\frac{\sqrt{\mathrm{1}+{u}}}{{u}}−\frac{\sqrt{\mathrm{1}−{u}}}{{u}}\right){du}= \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left[\mathrm{ln}\:\mid\frac{\mathrm{1}−\sqrt{\mathrm{1}+{u}}}{\mathrm{1}−\sqrt{\mathrm{1}−{u}}}\mid\:+\sqrt{\mathrm{1}+{u}}−\sqrt{\mathrm{1}−{u}}\right]_{−\mathrm{1}} ^{\mathrm{1}} = \\ $$$$=\mathrm{2}−\sqrt{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
