
Question Number 175351 by cortano1 last updated on 28/Aug/22
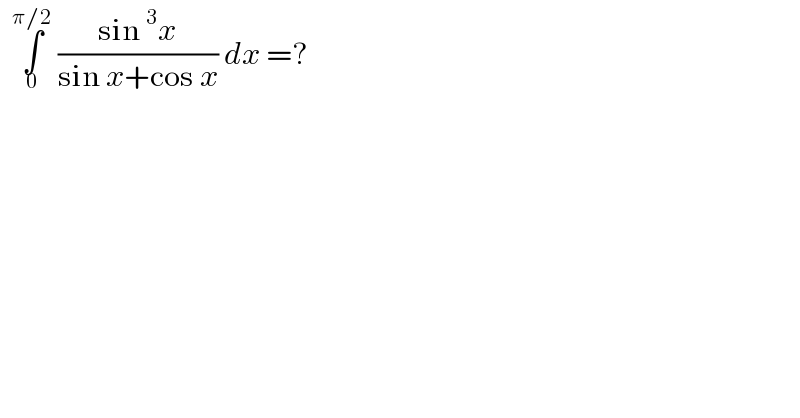
$$\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{sin}\:^{\mathrm{3}} {x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx}\:=? \\ $$
Answered by som(math1967) last updated on 28/Aug/22
![I=∫_0 ^(π/2) ((sin^3 ((π/2)+0−x)dx)/(sin((π/2)+0−x)+cos((π/2)+0−x))) =∫_0 ^(π/2) ((cos^3 xdx)/(cosx+sinx)) 2I=∫_0 ^(π/2) ((sin^3 x+cos^3 x)/(sinx+cosx))dx 2I=∫_0 ^(π/2) (sin^2 x−sinxcox+cos^2 x)dx 2I=∫_0 ^(π/2) dx−(1/2)∫_0 ^(π/2) sin2xdx 2I=[x+((cos2x)/4)]_0 ^(π/2) 2I=((π/2)−(1/4))−(0+(1/4)) I=(π/4) −(1/4)](Q175357.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{3}} \left(\frac{\pi}{\mathrm{2}}+\mathrm{0}−{x}\right){dx}}{{sin}\left(\frac{\pi}{\mathrm{2}}+\mathrm{0}−{x}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}+\mathrm{0}−{x}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{3}} {xdx}}{{cosx}+{sinx}} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}}{{sinx}+{cosx}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sin}^{\mathrm{2}} {x}−{sinxcox}+{cos}^{\mathrm{2}} {x}\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}\mathrm{2}{xdx} \\ $$$$\mathrm{2}{I}=\left[{x}+\frac{{cos}\mathrm{2}{x}}{\mathrm{4}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{2}{I}=\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right)−\left(\mathrm{0}+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$${I}=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by cortano1 last updated on 28/Aug/22

$${by}\:{King}\:{Formula} \\ $$
Commented by som(math1967) last updated on 28/Aug/22

$${yes} \\ $$
