Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 205558 by universe last updated on 24/Mar/24

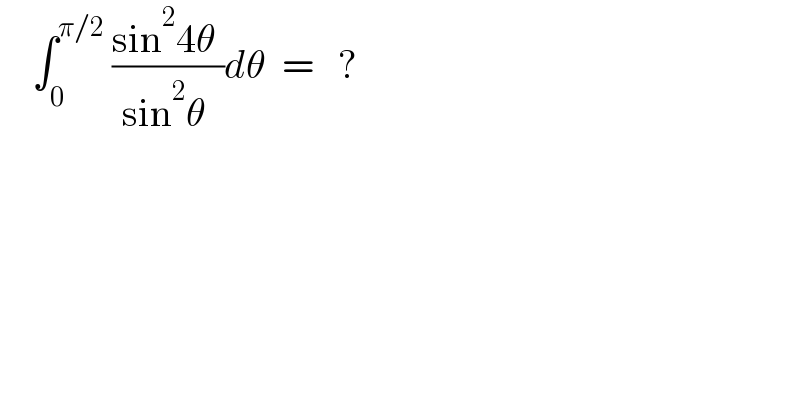
∫_0 ^(π/2) ((sin^2 4θ )/(sin^2 θ ))dθ = ?

$$\:\:\:\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{4}\theta\:}{\mathrm{sin}^{\mathrm{2}} \theta\:}{d}\theta\:\:=\:\:\:? \\ $$

Answered by Berbere last updated on 24/Mar/24

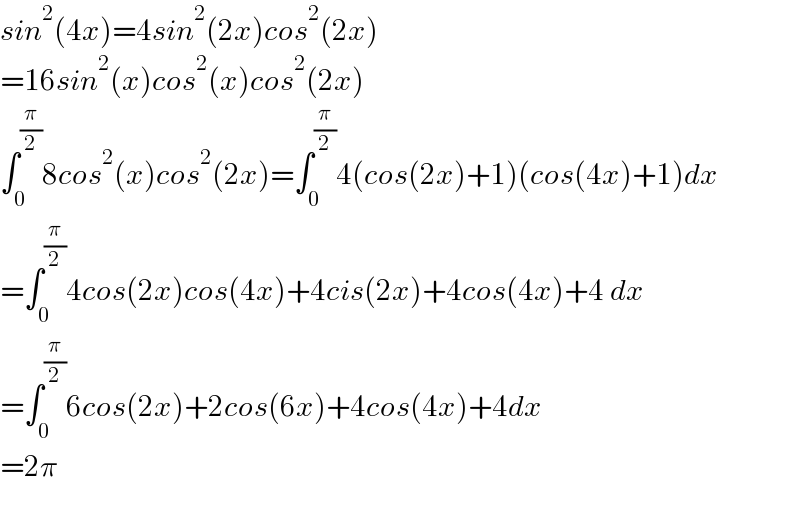
sin^2 (4x)=4sin^2 (2x)cos^2 (2x) =16sin^2 (x)cos^2 (x)cos^2 (2x) ∫_0 ^(π/2) 8cos^2 (x)cos^2 (2x)=∫_0 ^(π/2) 4(cos(2x)+1)(cos(4x)+1)dx =∫_0 ^(π/2) 4cos(2x)cos(4x)+4cis(2x)+4cos(4x)+4 dx =∫_0 ^(π/2) 6cos(2x)+2cos(6x)+4cos(4x)+4dx =2π

$${sin}^{\mathrm{2}} \left(\mathrm{4}{x}\right)=\mathrm{4}{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right){cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right) \\ $$$$=\mathrm{16}{sin}^{\mathrm{2}} \left({x}\right){cos}^{\mathrm{2}} \left({x}\right){cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{8}{cos}^{\mathrm{2}} \left({x}\right){cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{4}\left({cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\right)\left({cos}\left(\mathrm{4}{x}\right)+\mathrm{1}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{4}{cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{4}{x}\right)+\mathrm{4}{cis}\left(\mathrm{2}{x}\right)+\mathrm{4}{cos}\left(\mathrm{4}{x}\right)+\mathrm{4}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{6}{cos}\left(\mathrm{2}{x}\right)+\mathrm{2}{cos}\left(\mathrm{6}{x}\right)+\mathrm{4}{cos}\left(\mathrm{4}{x}\right)+\mathrm{4}{dx} \\ $$$$=\mathrm{2}\pi \\ $$$$ \\ $$

Commented by Frix last updated on 24/Mar/24

((sin^2 4x)/(sin^2 x))=2cos 6x +4cos 4x +6cos 2x +4 ⇒ ∫_0 ^(π/2) ((sin^2 4x)/(sin^2 x))dx= =[(1/3)sin 6x +sin 4x +3sin 2x +4x]_0 ^(π/2) =2π

$$\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{4}{x}}{\mathrm{sin}^{\mathrm{2}} \:{x}}=\mathrm{2cos}\:\mathrm{6}{x}\:+\mathrm{4cos}\:\mathrm{4}{x}\:+\mathrm{6cos}\:\mathrm{2}{x}\:+\mathrm{4} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{4}{x}}{\mathrm{sin}^{\mathrm{2}} \:{x}}{dx}= \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\mathrm{6}{x}\:+\mathrm{sin}\:\mathrm{4}{x}\:+\mathrm{3sin}\:\mathrm{2}{x}\:+\mathrm{4}{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{2}\pi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com