
Question Number 141388 by cesarL last updated on 18/May/21
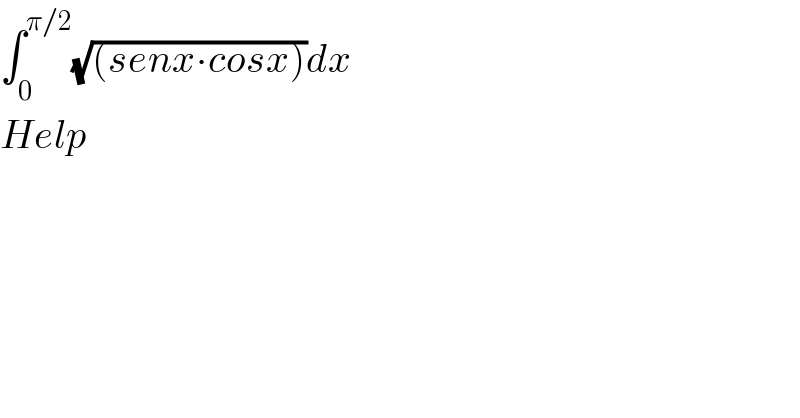
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \sqrt{\left({senx}\centerdot{cosx}\right)}{dx} \\ $$$${Help} \\ $$
Answered by Dwaipayan Shikari last updated on 18/May/21
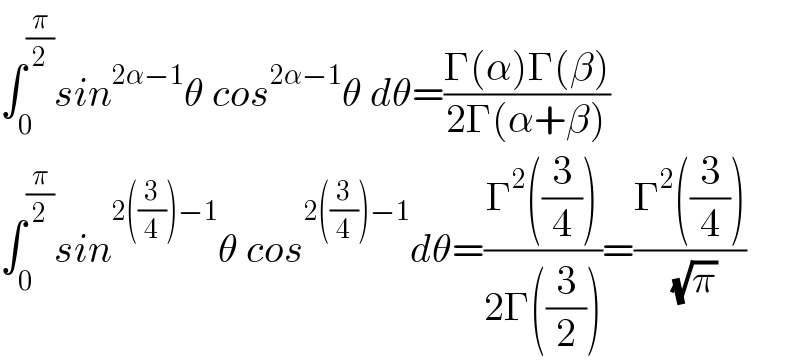
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}\alpha−\mathrm{1}} \theta\:{cos}^{\mathrm{2}\alpha−\mathrm{1}} \theta\:{d}\theta=\frac{\Gamma\left(\alpha\right)\Gamma\left(\beta\right)}{\mathrm{2}\Gamma\left(\alpha+\beta\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\mathrm{1}} \theta\:{cos}^{\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\mathrm{1}} {d}\theta=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\mathrm{2}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\:\sqrt{\pi}}\: \\ $$
