
Question Number 89161 by M±th+et£s last updated on 15/Apr/20
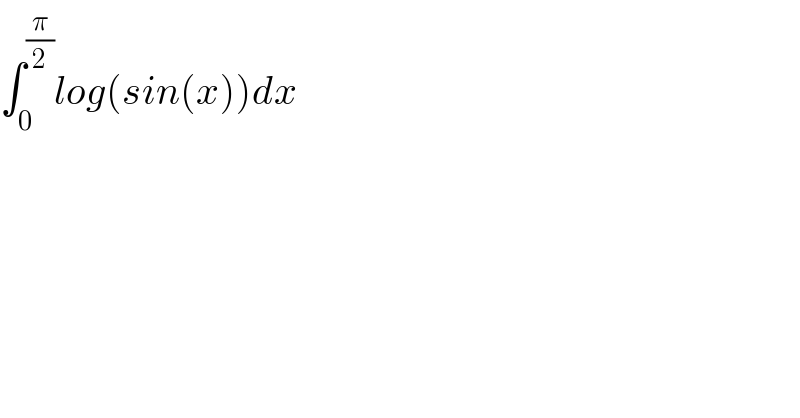
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}\left({x}\right)\right){dx} \\ $$
Commented by niroj last updated on 15/Apr/20
![I=∫_0 ^(π/2) log sin x dx.....(i) = ∫_0 ^(π/2) log sin((π/2)−x) dx [∵ ∫_0 ^( a) f(c)dx=∫_0 ^a f(a−c)dx] I = ∫_0 ^(π/2) log cos x dx.....(ii) added (i)+(ii) 2I= ∫_0 ^(π/2) (log sin x+log cos x)dx 2I= ∫_0 ^(π/2) log sin x.cos xdx 2I= ∫_0 ^(π/2) log( ((2sin xcos x)/2))dx 2I= ∫^(π/2) _0 log sin2x dx−∫_0 ^(π/2) log 2 dx put 2x= t 2dx=dt dx=(dt/2) if x=(π/2) then t=π if x=0 then t=0 ∫_0 ^π log sin t.(dt/2) =(1/2)∫_0 ^( π) log sint dt = (1/2)×2∫_0 ^(π/2) log sint dt ∴ ∫_0 ^(π/2) log sint dt = ∫_0 ^(π/2) log sin x dx=I 2I= I−log 2∫_0 ^(π/2) dx 2I−I = −log 2[ x]_0 ^(π/2) I = log 2^(−1) [ (π/2)−0] I = (π/2) log (1/2) //.](Q89164.png)
$$\:\:\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{log}\:\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}.....\left(\mathrm{i}\right) \\ $$$$\:\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{log}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)\:\mathrm{dx}\:\:\:\left[\because\:\int_{\mathrm{0}} ^{\:\boldsymbol{{a}}} \boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{c}}\right)\boldsymbol{\mathrm{dx}}=\int_{\mathrm{0}} ^{\boldsymbol{\mathrm{a}}} \boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{c}}\right)\boldsymbol{\mathrm{dx}}\right] \\ $$$$\:\mathrm{I}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{log}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}.....\left(\mathrm{ii}\right) \\ $$$$\:\mathrm{added}\:\left(\mathrm{i}\right)+\left(\mathrm{ii}\right) \\ $$$$\:\:\mathrm{2I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{log}\:\mathrm{sin}\:\mathrm{x}+\mathrm{log}\:\mathrm{cos}\:\mathrm{x}\right)\mathrm{dx} \\ $$$$\:\:\mathrm{2I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{log}\:\mathrm{sin}\:\mathrm{x}.\mathrm{cos}\:\mathrm{xdx} \\ $$$$\:\:\:\mathrm{2I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{log}\left(\:\frac{\mathrm{2sin}\:\mathrm{xcos}\:\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$\:\:\:\mathrm{2I}=\:\underset{\mathrm{0}} {\int}^{\frac{\pi}{\mathrm{2}}} \:\mathrm{log}\:\mathrm{sin2x}\:\mathrm{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{log}\:\mathrm{2}\:\mathrm{dx} \\ $$$$\:\:\:\:\:\mathrm{put}\:\mathrm{2x}=\:\mathrm{t}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{2dx}=\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{dx}=\frac{\mathrm{dt}}{\mathrm{2}} \\ $$$$\:\:\:\mathrm{if}\:\mathrm{x}=\frac{\pi}{\mathrm{2}}\:\mathrm{then}\:\mathrm{t}=\pi \\ $$$$\:\:\mathrm{if}\:\mathrm{x}=\mathrm{0}\:\mathrm{then}\:\mathrm{t}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{log}\:\mathrm{sin}\:\mathrm{t}.\frac{\mathrm{dt}}{\mathrm{2}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi} \mathrm{log}\:\mathrm{sint}\:\mathrm{dt} \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{log}\:\mathrm{sint}\:\mathrm{dt} \\ $$$$\:\:\therefore\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{log}\:\mathrm{sint}\:\mathrm{dt}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{log}\:\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}=\mathrm{I} \\ $$$$\:\:\mathrm{2I}=\:\mathrm{I}−\mathrm{log}\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{dx} \\ $$$$\mathrm{2I}−\mathrm{I}\:=\:−\mathrm{log}\:\mathrm{2}\left[\:\mathrm{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:\:\mathrm{I}\:=\:\:\mathrm{log}\:\mathrm{2}^{−\mathrm{1}} \left[\:\frac{\pi}{\mathrm{2}}−\mathrm{0}\right] \\ $$$$\:\:\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}\:\mathrm{log}\:\frac{\mathrm{1}}{\mathrm{2}}\://. \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$\: \\ $$
Commented by M±th+et£s last updated on 15/Apr/20
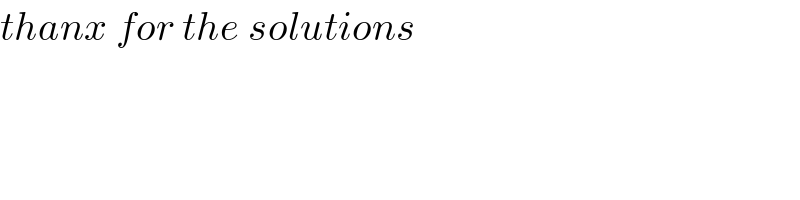
$${thanx}\:{for}\:{the}\:{solutions} \\ $$
Answered by TANMAY PANACEA. last updated on 15/Apr/20
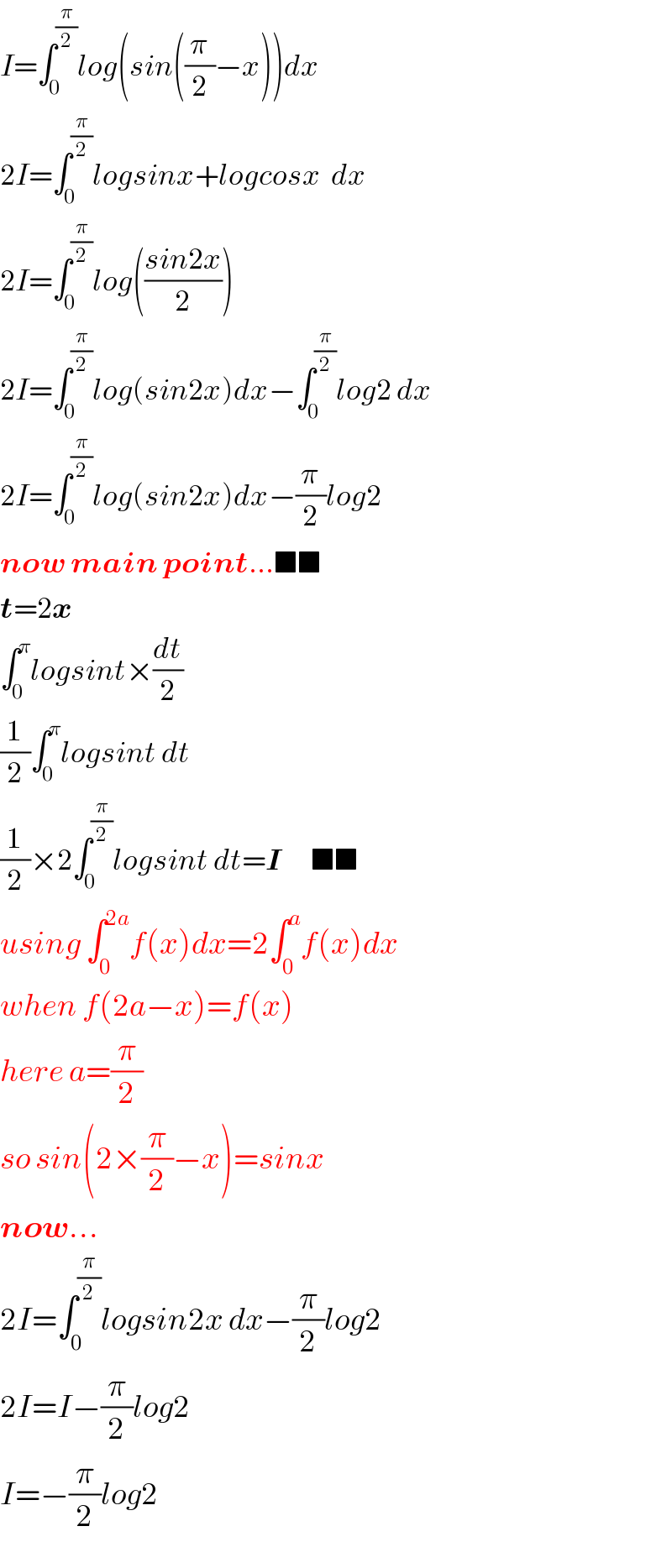
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right){dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {logsinx}+{logcosx}\:\:{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}\mathrm{2}{x}\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\mathrm{2}\:{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}\mathrm{2}{x}\right){dx}−\frac{\pi}{\mathrm{2}}{log}\mathrm{2} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{main}}\:\boldsymbol{{point}}...\blacksquare\blacksquare \\ $$$$\boldsymbol{{t}}=\mathrm{2}\boldsymbol{{x}} \\ $$$$\int_{\mathrm{0}} ^{\pi} {logsint}×\frac{{dt}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} {logsint}\:{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {logsint}\:{dt}=\boldsymbol{{I}}\:\:\:\:\:\:\blacksquare\blacksquare \\ $$$${using}\:\int_{\mathrm{0}} ^{\mathrm{2}{a}} {f}\left({x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx} \\ $$$${when}\:{f}\left(\mathrm{2}{a}−{x}\right)={f}\left({x}\right) \\ $$$${here}\:{a}=\frac{\pi}{\mathrm{2}} \\ $$$${so}\:{sin}\left(\mathrm{2}×\frac{\pi}{\mathrm{2}}−{x}\right)={sinx} \\ $$$$\boldsymbol{{now}}... \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {logsin}\mathrm{2}{x}\:{dx}−\frac{\pi}{\mathrm{2}}{log}\mathrm{2} \\ $$$$\mathrm{2}{I}={I}−\frac{\pi}{\mathrm{2}}{log}\mathrm{2} \\ $$$${I}=−\frac{\pi}{\mathrm{2}}{log}\mathrm{2} \\ $$
