Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 139399 by mathsuji last updated on 26/Apr/21

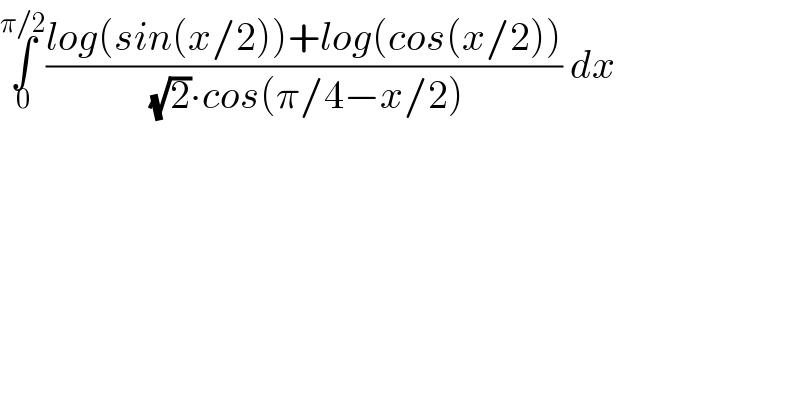
∫_0 ^(π/2) ((log(sin(x/2))+log(cos(x/2)))/( (√2)∙cos(π/4−x/2))) dx

$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{log}\left({sin}\left({x}/\mathrm{2}\right)\right)+{log}\left({cos}\left({x}/\mathrm{2}\right)\right)}{\:\sqrt{\mathrm{2}}\centerdot{cos}\left(\pi/\mathrm{4}−{x}/\mathrm{2}\right)}\:{dx} \\ $$

Answered by Ar Brandon last updated on 26/Apr/21

Let u=(π/2)−x

$$\mathrm{Let}\:{u}=\frac{\pi}{\mathrm{2}}−{x} \\ $$

Answered by Ar Brandon last updated on 26/Apr/21

I=∫_0 ^(π/2) ((ln(sin(x/2))+ln(cos(x/2)))/( (√2)cos((π/4)−(x/2))))dx =∫_0 ^(π/2) ((ln(sin(x/2)cos(x/2)))/( (√2)cos((1/2)((π/2)−x))))dx=∫_0 ^(π/2) ((ln((1/2))+ln(sinx))/( (√2)cos((1/2)((π/2)−x))))dx =−((ln2)/( (√2)))∫_0 ^(π/2) (dx/(cos((1/2)((π/2)−x))))+(1/( (√2)))∫_0 ^(π/2) ((ln(sinx))/(cos((1/2)((π/2)−x))))dx =(√2)ln2[ln∣sec((π/4)−(x/2))+tan((π/4)−(x/2))∣]+(1/( (√2)))J J=∫_0 ^(π/2) ((ln(cosx))/(cos((x/2))))dx

$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{ln}\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}\right)+\mathrm{ln}\left(\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{ln}\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{ln}\left(\mathrm{sin}{x}\right)}{\:\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)}{dx} \\ $$$$\:\:=−\frac{\mathrm{ln2}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{ln}\left(\mathrm{sin}{x}\right)}{\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)}{dx} \\ $$$$\:\:=\sqrt{\mathrm{2}}\mathrm{ln2}\left[\mathrm{ln}\mid\mathrm{sec}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)+\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\mid\right]+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathcal{J} \\ $$$$\mathcal{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{ln}\left(\mathrm{cos}{x}\right)}{\mathrm{cos}\left(\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$

Answered by mathmax by abdo last updated on 26/Apr/21

I =∫_0 ^(π/2) ((log(sin((x/2)))+log(cos((x/2))))/( (√2)cos((π/4)−(x/2))))dx ⇒ I =∫_0 ^(π/(2 )) ((log(((sinx)/2)))/( (√2)cos((π/4)−(x/2))))dx =_((π/4)−(x/2)=t) ∫_(π/4) ^o ((log((1/2)sin((π/2)−2t)))/( (√2)cost))(−2)dt =(√2)∫_0 ^(π/4) ((log(cos(2t))−log2)/(cost))dt =(√2)∫_0 ^(π/4) ((log(cos(2t)))/(cost))dt−(√2)log(2)∫_0 ^(π/4) (dt/(cost)) ∫_0 ^(π/(4 )) ((log(cos(2t)))/(cost))dt =∫_0 ^(π/4) ((log(2cos^2 t−1))/(cost))dt =_(cost=x) ∫_1 ^(1/( (√2))) ((log(2x^2 −1))/x)(−(dx/( (√(1−x^2 ))))) =∫_(1/( (√2))) ^1 ((log(2x^2 −1))/(x(√(1−x^2 ))))dx let f(a)=∫_(1/( (√2))) ^1 ((log(2x^2 −a))/(x(√(1−x^2 ))))dx with o<a<(√2) f^′ (a)=−∫_(1/( (√2))) ^1 (1/((2x^2 −a)x(√(1−x^2 ))))dx =_(x=sinθ) − ∫_(π/4) ^(π/2) ((cosθ dθ)/((2sin^2 θ−1)sinθ.cosθ)) =−∫_(π/4) ^(π/2) (dθ/(sinθ(2sin^2 θ−a))) F(u)=(1/(u(2u^2 −1))) =(1/(u((√2)u−(√a))((√2)u+(√a))))=(m/u)+(b/(u(√2)−(√a)))+(c/(u(√2)+(√a))) ⇒f^′ (a) =−m∫_(π/4) ^(π/2) (dθ/(sinθ))−b∫_(π/4) ^(π/2) (dθ/( (√2)sinθ −(√a)))−c∫_(π/4) ^(π/2) (dθ/( (√2)sinθ +(√a))) ∫_(π/4) ^(π/2) (dθ/(sinθ)) =_(tan((θ/2))=t) ∫_((√2)−1) ^1 ((2dt)/((1+t^2 )×((2t)/(1+t^2 ))))=∫_((√2)−1) ^1 (dt/t) =−log((√2)−1) ∫_(π/4) ^(π/2) (dθ/( (√2)sinθ−(√a))) =_(tan((θ/2))=y) ∫_((√2)−1) ^1 ((2dy)/((1+y^2 )((√2)((2y)/(1+y^2 ))−(√a)))) =2∫_((√2)−1) ^1 (dy/(2(√2)y−(√a)−(√a)y^2 )) =−2∫_((√2)−1) ^1 (dy/( (√a)y^2 −2(√2)y+(√a))) Δ^′ =2−a^2 >0 ⇒y_1 =(((√2)+(√(2−a^2 )))/( (√a))) and y_2 =(((√2)−(√(2−a^2 )))/( (√a))) ....be continued....

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{log}\left(\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\mathrm{log}\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)}{\:\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}\right)}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}\:}} \frac{\mathrm{log}\left(\frac{\mathrm{sinx}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}\right)}\mathrm{dx}\:=_{\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}} \:\:\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{o}} \:\frac{\mathrm{log}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2t}\right)\right)}{\:\sqrt{\mathrm{2}}\mathrm{cost}}\left(−\mathrm{2}\right)\mathrm{dt} \\ $$$$=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{log}\left(\mathrm{cos}\left(\mathrm{2t}\right)\right)−\mathrm{log2}}{\mathrm{cost}}\mathrm{dt} \\ $$$$=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{log}\left(\mathrm{cos}\left(\mathrm{2t}\right)\right)}{\mathrm{cost}}\mathrm{dt}−\sqrt{\mathrm{2}}\mathrm{log}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{dt}}{\mathrm{cost}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}\:}} \frac{\mathrm{log}\left(\mathrm{cos}\left(\mathrm{2t}\right)\right)}{\mathrm{cost}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{log}\left(\mathrm{2cos}^{\mathrm{2}} \mathrm{t}−\mathrm{1}\right)}{\mathrm{cost}}\mathrm{dt} \\ $$$$=_{\mathrm{cost}=\mathrm{x}} \:\:\:\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \:\:\:\frac{\mathrm{log}\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{x}}\left(−\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\right) \\ $$$$=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{a}\right)}{\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\mathrm{with}\:\mathrm{o}<\mathrm{a}<\sqrt{\mathrm{2}} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\left(\mathrm{2x}^{\mathrm{2}} −\mathrm{a}\right)\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx} \\ $$$$=_{\mathrm{x}=\mathrm{sin}\theta} \:\:−\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{\mathrm{cos}\theta\:\mathrm{d}\theta}{\left(\mathrm{2sin}^{\mathrm{2}} \theta−\mathrm{1}\right)\mathrm{sin}\theta.\mathrm{cos}\theta} \\ $$$$=−\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{d}\theta}{\mathrm{sin}\theta\left(\mathrm{2sin}^{\mathrm{2}} \theta−\mathrm{a}\right)} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{1}}{\mathrm{u}\left(\mathrm{2u}^{\mathrm{2}} −\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{u}\left(\sqrt{\mathrm{2}}\mathrm{u}−\sqrt{\mathrm{a}}\right)\left(\sqrt{\mathrm{2}}\mathrm{u}+\sqrt{\mathrm{a}}\right)}=\frac{\mathrm{m}}{\mathrm{u}}+\frac{\mathrm{b}}{\mathrm{u}\sqrt{\mathrm{2}}−\sqrt{\mathrm{a}}}+\frac{\mathrm{c}}{\mathrm{u}\sqrt{\mathrm{2}}+\sqrt{\mathrm{a}}} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\mathrm{m}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{d}\theta}{\mathrm{sin}\theta}−\mathrm{b}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{d}\theta}{\:\sqrt{\mathrm{2}}\mathrm{sin}\theta\:−\sqrt{\mathrm{a}}}−\mathrm{c}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{d}\theta}{\:\sqrt{\mathrm{2}}\mathrm{sin}\theta\:+\sqrt{\mathrm{a}}} \\ $$$$\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{d}\theta}{\mathrm{sin}\theta}\:=_{\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\int_{\sqrt{\mathrm{2}}−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}=\int_{\sqrt{\mathrm{2}}−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}} \\ $$$$=−\mathrm{log}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{d}\theta}{\:\sqrt{\mathrm{2}}\mathrm{sin}\theta−\sqrt{\mathrm{a}}}\:=_{\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)=\mathrm{y}} \:\:\int_{\sqrt{\mathrm{2}}−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\sqrt{\mathrm{2}}\frac{\mathrm{2y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }−\sqrt{\mathrm{a}}\right)} \\ $$$$=\mathrm{2}\int_{\sqrt{\mathrm{2}}−\mathrm{1}} ^{\mathrm{1}} \:\:\frac{\mathrm{dy}}{\mathrm{2}\sqrt{\mathrm{2}}\mathrm{y}−\sqrt{\mathrm{a}}−\sqrt{\mathrm{a}}\mathrm{y}^{\mathrm{2}} }\:=−\mathrm{2}\int_{\sqrt{\mathrm{2}}−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{dy}}{\:\sqrt{\mathrm{a}}\mathrm{y}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{y}+\sqrt{\mathrm{a}}} \\ $$$$\Delta^{'} \:=\mathrm{2}−\mathrm{a}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\mathrm{y}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}−\mathrm{a}^{\mathrm{2}} }}{\:\sqrt{\mathrm{a}}}\:\mathrm{and}\:\mathrm{y}_{\mathrm{2}} =\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}−\mathrm{a}^{\mathrm{2}} }}{\:\sqrt{\mathrm{a}}} \\ $$$$....\mathrm{be}\:\mathrm{continued}.... \\ $$

Answered by qaz last updated on 27/Apr/21

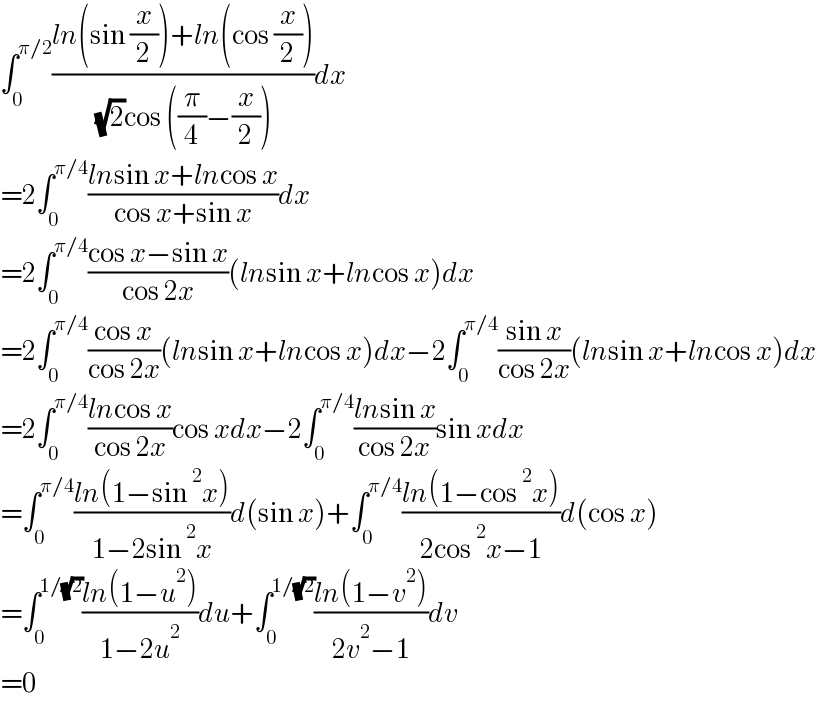
∫_0 ^(π/2) ((ln(sin (x/2))+ln(cos (x/2)))/( (√2)cos ((π/4)−(x/2))))dx =2∫_0 ^(π/4) ((lnsin x+lncos x)/(cos x+sin x))dx =2∫_0 ^(π/4) ((cos x−sin x)/(cos 2x))(lnsin x+lncos x)dx =2∫_0 ^(π/4) ((cos x)/(cos 2x))(lnsin x+lncos x)dx−2∫_0 ^(π/4) ((sin x)/(cos 2x))(lnsin x+lncos x)dx =2∫_0 ^(π/4) ((lncos x)/(cos 2x))cos xdx−2∫_0 ^(π/4) ((lnsin x)/(cos 2x))sin xdx =∫_0 ^(π/4) ((ln(1−sin^2 x))/(1−2sin^2 x))d(sin x)+∫_0 ^(π/4) ((ln(1−cos^2 x))/(2cos^2 x−1))d(cos x) =∫_0 ^(1/(√2)) ((ln(1−u^2 ))/(1−2u^2 ))du+∫_0 ^(1/(√2)) ((ln(1−v^2 ))/(2v^2 −1))dv =0

$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\left(\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)+{ln}\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{ln}\mathrm{sin}\:{x}+{ln}\mathrm{cos}\:{x}}{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}}\left({ln}\mathrm{sin}\:{x}+{ln}\mathrm{cos}\:{x}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{\mathrm{cos}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}}\left({ln}\mathrm{sin}\:{x}+{ln}\mathrm{cos}\:{x}\right){dx}−\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}}\left({ln}\mathrm{sin}\:{x}+{ln}\mathrm{cos}\:{x}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{ln}\mathrm{cos}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}}\mathrm{cos}\:{xdx}−\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{ln}\mathrm{sin}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}}\mathrm{sin}\:{xdx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{ln}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)}{\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}}{d}\left(\mathrm{sin}\:{x}\right)+\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{ln}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}}{d}\left(\mathrm{cos}\:{x}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}/\sqrt{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{2}{u}^{\mathrm{2}} }{du}+\int_{\mathrm{0}} ^{\mathrm{1}/\sqrt{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}−{v}^{\mathrm{2}} \right)}{\mathrm{2}{v}^{\mathrm{2}} −\mathrm{1}}{dv} \\ $$$$=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com