
Question Number 313 by Vishal Bhardwaj last updated on 25/Jan/15
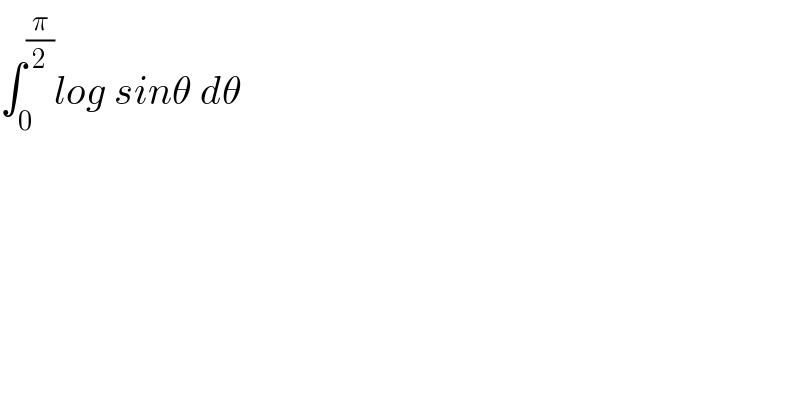
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\:{sin}\theta\:{d}\theta \\ $$
Answered by prakash jain last updated on 20/Dec/14

$${I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{sin}\:\theta{d}\theta\:\:\:\:\:\:\:\:.....\left({i}\right) \\ $$$$\mathrm{put}\:\theta=\frac{\pi}{\mathrm{2}}−\alpha,\:{d}\theta=−{d}\alpha \\ $$$${I}=\int_{\pi/\mathrm{2}} ^{\mathrm{0}} \mathrm{ln}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\alpha\right)\left(−{d}\alpha\right) \\ $$$$=−\int_{\pi/\mathrm{2}} ^{\mathrm{0}} \mathrm{ln}\:\mathrm{cos}\:\alpha{d}\alpha=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{cos}\:\alpha{d}\alpha \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{cos}\:\theta{d}\theta\:\:\:\:\:\:\:....\left({ii}\right) \\ $$$$\mathrm{add}\:\left({i}\right)\:\mathrm{and}\:\left({ii}\right) \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{ln}\:\mathrm{sin}\:\theta+\mathrm{ln}\:\mathrm{cos}\:\theta\right){d}\theta \\ $$$$\mathrm{2I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\:{d}\theta \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{ln}\:\mathrm{sin}\:\mathrm{2}\theta\:−\mathrm{ln}\:\mathrm{2}\right)\:{d}\theta\:\:\:\:\:\: \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{sin}\:\mathrm{2}\theta\:{d}\theta−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{2}\:{d}\theta\:\:\:\:\:\: \\ $$$$\mathrm{In}\:\mathrm{first}\:\mathrm{integral}\:\mathrm{put}\:\mathrm{2}\theta=\beta\:,\mathrm{2}{d}\theta={d}\beta\:\mathrm{so} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{one}\:\mathrm{now}\:\mathrm{with}\:\mathrm{updated}\:\mathrm{limits} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\frac{{d}\beta}{\mathrm{2}}−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{2}\:{d}\theta\:\: \\ $$$$\mathrm{2}{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{2}\:{d}\theta\:\:....\left({iii}\right) \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{will}\:\mathrm{evaluate}\:\mathrm{first}\:\mathrm{integral} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta+\int_{\pi/\mathrm{2}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta=={I}+\int_{\pi/\mathrm{2}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta{d}\beta \\ $$$$\mathrm{put}\:\beta=\pi−{t}\:{d}\beta=−{dt} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta=={I}+\int_{\pi/\mathrm{2}} ^{\mathrm{0}} \mathrm{ln}\:\mathrm{sin}\:\left(\pi−{t}\right)\left(−{dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta=={I}−\int_{\pi/\mathrm{2}} ^{\mathrm{0}} \mathrm{ln}\:\mathrm{sin}\:{tdt} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta=={I}+\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{sin}\:{t}\:{dt} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\:\mathrm{sin}\:\beta\:{d}\beta=={I}+{I}=\mathrm{2}{I}\:\:\:\:\:....\left({iv}\right) \\ $$$$\mathrm{putting}\:\mathrm{this}\:\mathrm{value}\:\mathrm{in}\:\left({iii}\right) \\ $$$$\mathrm{2}{I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{I}\right)−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}\:\mathrm{2}{d}\theta \\ $$$$\mathrm{2}{I}={I}−\frac{\pi}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$$${I}=−\frac{\pi}{\mathrm{2}}\mathrm{ln}\:\mathrm{2} \\ $$
