Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 91493 by Zainal Arifin last updated on 01/May/20

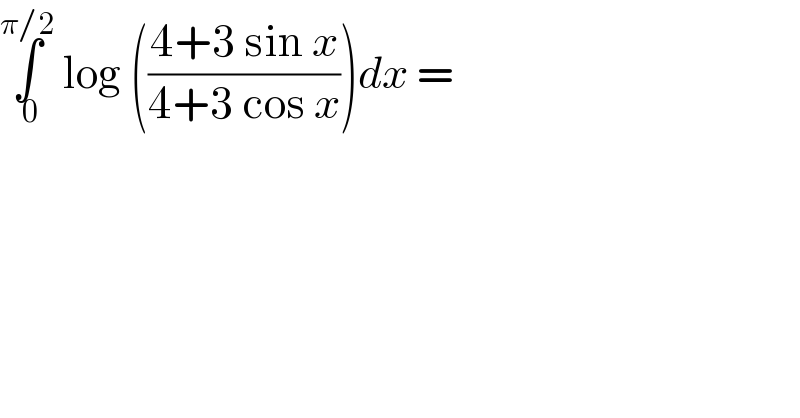
∫_( 0) ^(π/2) log (((4+3 sin x)/(4+3 cos x)))dx =

$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\mathrm{log}\:\left(\frac{\mathrm{4}+\mathrm{3}\:\mathrm{sin}\:{x}}{\mathrm{4}+\mathrm{3}\:\mathrm{cos}\:{x}}\right){dx}\:= \\ $$

Commented by mathmax by abdo last updated on 01/May/20

I =∫_0 ^(π/2) ln(((1+(3/4)sinx)/(1+(3/4)cosx))) =∫_0 ^(π/2) ln(1+(3/4)sinx)−∫_0 ^(π/2) ln(1+(3/4)cosx) let f(a) =∫_0 ^(π/2) ln(1+a sinx) with 0<a<1 f^′ (a) =∫_0 ^(π/2) ((sinx)/(1+asinx))dx =(1/a)∫_0 ^(π/2) ((1+asinx−1)/(1+asinx))dx =(π/(2a))−(1/a)∫_0 ^(π/2) (dx/(1+asinx)) but ∫_0 ^(π/2) (dx/(1+asinx)) =_(tan((x/2))=t) ∫_0 ^1 ((2dt)/((1+t^2 )(1+a((2t)/(1+t^2 ))))) =2∫_0 ^1 (dt/(1+t^2 +2at)) =2 ∫_0 ^1 (dt/(t^2 +2at +1)) =2 ∫_0 ^1 (dt/((t+a)^2 +1−a^2 )) =_(t+a =(√(1−a^2 ))u) 2 ∫_(a/(√(1−a^2 ))) ^((1+a)/(√(1−a^2 ))) (((√(1−a^2 ))du)/((1−a^2 )(1+u^2 ))) =(2/(√(1−a^2 )))( arctan(((1+a)/(√(1−a^2 ))))−arctan((a/(√(1−a^2 ))))) ⇒ f(a) =(π/2)ln(a)−2 ∫ (1/(a(√(1−a^2 )))) arctan(((1+a)/(√(1−a^2 ))))da +2∫ (1/(a(√(1−a^2 )))) arctan((a/(√(1−a^2 )))) +c we have ∫ (1/(a(√(1−a^2 )))) arctan((a/(√(1−a^2 )))) =_(a=sinx) ∫ (1/(sinx cosx))arctan(((sinx)/(cosx)))cosxdx =∫ (x/(sinx)) dx ∫ (1/(a(√(1−a^2 )))) arctan(((1+a)/(√(1−a^2 ))))da =_(a =cosx) − ∫(1/(cosx sinx))arctan(((1+cosx)/(sinx)))sinxdx =−∫ (1/(cosx)) arctan(((2cos^2 ((x/2)))/(2sin((x/2))cos((x/2)))))dx =−∫ (1/(cosx)) arctan((1/(tanx)))dx =−∫ (1/(cosx))((π/2) −x) =−(π/2)∫ (dx/(cosx)) +∫ (x/(cosx))dx....be continued...

$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\frac{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}{sinx}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}{cosx}}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}{sinx}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}{cosx}\right) \\ $$$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{a}\:{sinx}\right)\:\:{with}\:\mathrm{0}<{a}<\mathrm{1} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sinx}}{\mathrm{1}+{asinx}}{dx}\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{asinx}−\mathrm{1}}{\mathrm{1}+{asinx}}{dx} \\ $$$$=\frac{\pi}{\mathrm{2}{a}}−\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{1}+{asinx}}\:\:{but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{1}+{asinx}}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{at}}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{2}{at}\:+\mathrm{1}}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left({t}+{a}\right)^{\mathrm{2}} \:+\mathrm{1}−{a}^{\mathrm{2}} } \\ $$$$=_{{t}+{a}\:=\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }{u}} \:\:\:\:\:\mathrm{2}\:\int_{\frac{{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}} ^{\frac{\mathrm{1}+{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}} \:\:\:\:\:\:\frac{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }{du}}{\left(\mathrm{1}−{a}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\left(\:{arctan}\left(\frac{\mathrm{1}+{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right)−{arctan}\left(\frac{{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right)\right)\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}{ln}\left({a}\right)−\mathrm{2}\:\int\:\:\:\frac{\mathrm{1}}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{1}+{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right){da} \\ $$$$+\mathrm{2}\int\:\:\frac{\mathrm{1}}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:{arctan}\left(\frac{{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right)\:+{c}\:\:{we}\:{have} \\ $$$$\int\:\:\frac{\mathrm{1}}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:{arctan}\left(\frac{{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right)\:=_{{a}={sinx}} \:\:\int\:\frac{\mathrm{1}}{{sinx}\:{cosx}}{arctan}\left(\frac{{sinx}}{{cosx}}\right){cosxdx} \\ $$$$=\int\:\:\frac{{x}}{{sinx}}\:{dx} \\ $$$$\int\:\:\frac{\mathrm{1}}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{1}+{a}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\right){da}\:=_{{a}\:={cosx}} \:\:−\:\int\frac{\mathrm{1}}{{cosx}\:{sinx}}{arctan}\left(\frac{\mathrm{1}+{cosx}}{{sinx}}\right){sinxdx} \\ $$$$=−\int\:\:\frac{\mathrm{1}}{{cosx}}\:{arctan}\left(\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)}\right){dx} \\ $$$$=−\int\:\frac{\mathrm{1}}{{cosx}}\:{arctan}\left(\frac{\mathrm{1}}{{tanx}}\right){dx}\:=−\int\:\frac{\mathrm{1}}{{cosx}}\left(\frac{\pi}{\mathrm{2}}\:−{x}\right) \\ $$$$=−\frac{\pi}{\mathrm{2}}\int\:\frac{{dx}}{{cosx}}\:+\int\:\:\frac{{x}}{{cosx}}{dx}....{be}\:{continued}... \\ $$$$ \\ $$

Answered by MJS last updated on 01/May/20

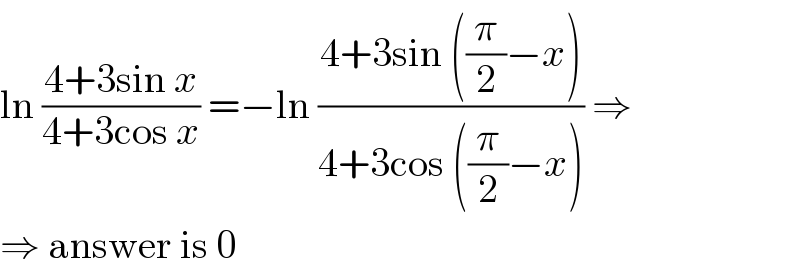
ln ((4+3sin x)/(4+3cos x)) =−ln ((4+3sin ((π/2)−x))/(4+3cos ((π/2)−x))) ⇒ ⇒ answer is 0

$$\mathrm{ln}\:\frac{\mathrm{4}+\mathrm{3sin}\:{x}}{\mathrm{4}+\mathrm{3cos}\:{x}}\:=−\mathrm{ln}\:\frac{\mathrm{4}+\mathrm{3sin}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{\mathrm{4}+\mathrm{3cos}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com