
Question Number 109129 by bemath last updated on 21/Aug/20
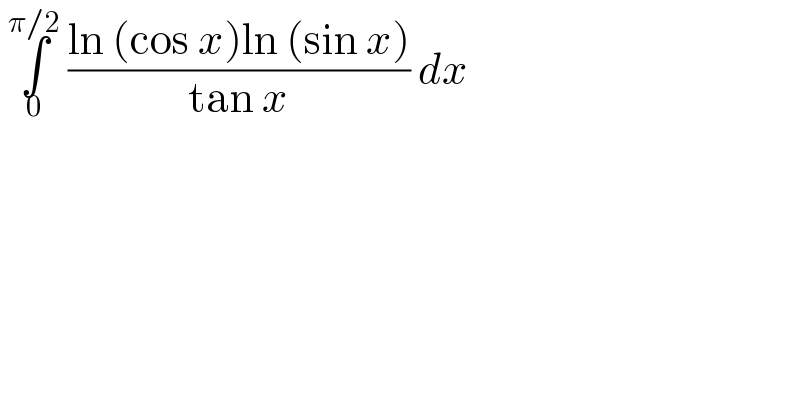
$$\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{ln}\:\left(\mathrm{cos}\:{x}\right)\mathrm{ln}\:\left(\mathrm{sin}\:{x}\right)}{\mathrm{tan}\:{x}}\:{dx} \\ $$
Answered by EmericGent last updated on 21/Aug/20
![= I =(1/2)∫_0 ^(π/2) ((ln(1-sin^2 x)ln(sin x))/(sin x)) cos x dx t = sin x ⇒ dt = cos x dx I = (1/2)∫_0 ^1 ((ln(1-t^2 )ln t)/t) dt I = −(1/2) ∫_0 ^1 ln t Σ_(k=1) ^∞ (t^(2k-1) /k) dt u = ln t ⇒ u′ = (1/t) v′ = (t^(2k-1) /k) ⇒ v = (t^(2k) /(2k^2 )) I = −(1/2)Σ_(k=1) ^∞ (1/(2k^2 ))(t^(2k) ln t]_0 ^1 −∫_0 ^1 t^(2k-1) dt) I = (1/2)Σ_(k=1) ^∞ ((t^(2k) ]_0 ^1 )/(4k^3 )) = (1/8) Σ_(k=1) ^∞ (1/k^3 ) = (1/8) ζ(3)](Q109131.png)
$$=\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\left(\mathrm{1}-{sin}^{\mathrm{2}} {x}\right){ln}\left({sin}\:{x}\right)}{{sin}\:{x}}\:{cos}\:{x}\:{dx} \\ $$$${t}\:=\:{sin}\:{x}\:\Rightarrow\:{dt}\:=\:{cos}\:{x}\:{dx} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}-{t}^{\mathrm{2}} \right){ln}\:{t}}{{t}}\:{dt} \\ $$$${I}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\:{t}\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}^{\mathrm{2}{k}-\mathrm{1}} }{{k}}\:{dt} \\ $$$${u}\:=\:{ln}\:{t}\:\Rightarrow\:{u}'\:=\:\frac{\mathrm{1}}{{t}} \\ $$$${v}'\:=\:\frac{{t}^{\mathrm{2}{k}-\mathrm{1}} }{{k}}\:\Rightarrow\:{v}\:=\:\frac{{t}^{\mathrm{2}{k}} }{\mathrm{2}{k}^{\mathrm{2}} } \\ $$$$\left.{I}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}^{\mathrm{2}} }\left({t}^{\mathrm{2}{k}} {ln}\:{t}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{k}-\mathrm{1}} \:{dt}\right) \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left.{t}^{\mathrm{2}{k}} \right]_{\mathrm{0}} ^{\mathrm{1}} }{\mathrm{4}{k}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{8}}\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{8}}\:\zeta\left(\mathrm{3}\right) \\ $$
