
Question Number 113821 by 675480065 last updated on 15/Sep/20
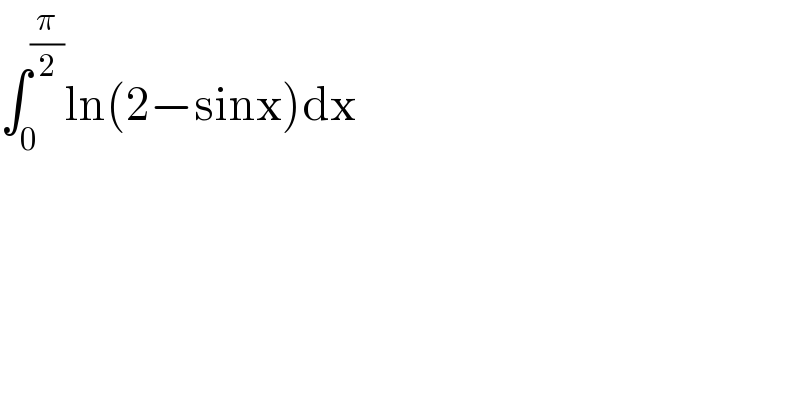
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2}−\mathrm{sinx}\right)\mathrm{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 15/Sep/20
![I(a)=∫_0 ^(π/2) log(2+asinx)dx I′(a)=∫_0 ^(π/2) ((sinx)/(2+asinx))dx I′(a)=(1/a)∫_0 ^(π/2) 1−(2/(2+asinx)) I′(a)=(π/(2a))−2∫_0 ^(π/2) (1/(2+asinx))dx I′(a)=(π/(2a))−4∫_0 ^(π/2) (1/(2+((2at)/(1+t^2 )))).(1/(1+t^2 ))dt (tan(x/2)=t) I′(a)=(π/(2a))−4∫_0 ^1 (1/(2+2t^2 +2at))dt I′(a)=(π/(2a))−2∫_0 ^1 (1/((t+(a/2))^2 +1−(a^2 /4)))dt I′(a)=(π/(2a))−2(1/( (√(1−(a^2 /4))))).[tan^(−1) ((2t+a)/( (√(4−a^2 ))))]_0 ^1 I(a)=(π/2)log(a)−∫(4/( (√(4−a^2 ))))(tan^(−1) (√((2+a)/(2−a))) −tan^(−1) (a/( (√(4−a^2 ))))).... .....](Q113843.png)
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{2}+{asinx}\right){dx} \\ $$$${I}'\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sinx}}{\mathrm{2}+{asinx}}{dx} \\ $$$${I}'\left({a}\right)=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}+{asinx}} \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{2}{a}}−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}+{asinx}}{dx} \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{2}{a}}−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{2}{at}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({tan}\frac{{x}}{\mathrm{2}}={t}\right) \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{2}{a}}−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}{at}}{dt} \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{2}{a}}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({t}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}{dt} \\ $$$${I}'\left({a}\right)=\frac{\pi}{\mathrm{2}{a}}−\mathrm{2}\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}}.\left[{tan}^{−\mathrm{1}} \frac{\mathrm{2}{t}+{a}}{\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}\left({a}\right)=\frac{\pi}{\mathrm{2}}{log}\left({a}\right)−\int\frac{\mathrm{4}}{\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\left({tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{2}+{a}}{\mathrm{2}−{a}}}\:−{tan}^{−\mathrm{1}} \frac{{a}}{\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\right).... \\ $$$$..... \\ $$
Answered by mathdave last updated on 15/Sep/20
![solution let A=∫_0 ^(π/2) ln[2(1−(1/2)sinx)]dx=ln2∫^(π/2) dx+∫^(π/2) (1−(1/2)sinx)dx A=(π/2)ln2+∫_0 ^(π/2) (1−(1/2)sinx)dx let I=∫_0 ^(π/2) (1−(1/2)sinx)dx.........(1)](Q113833.png)
$${solution}\: \\ $$$${let} \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left[\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}\right)\right]{dx}=\mathrm{ln2}\int^{\frac{\pi}{\mathrm{2}}} {dx}+\int^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}\right){dx} \\ $$$${A}=\frac{\pi}{\mathrm{2}}\mathrm{ln2}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}\right){dx} \\ $$$${let}\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}\right){dx}.........\left(\mathrm{1}\right) \\ $$
Commented by mathdave last updated on 15/Sep/20

Commented by mathdave last updated on 15/Sep/20

Commented by mathdave last updated on 15/Sep/20

Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by Olaf last updated on 15/Sep/20
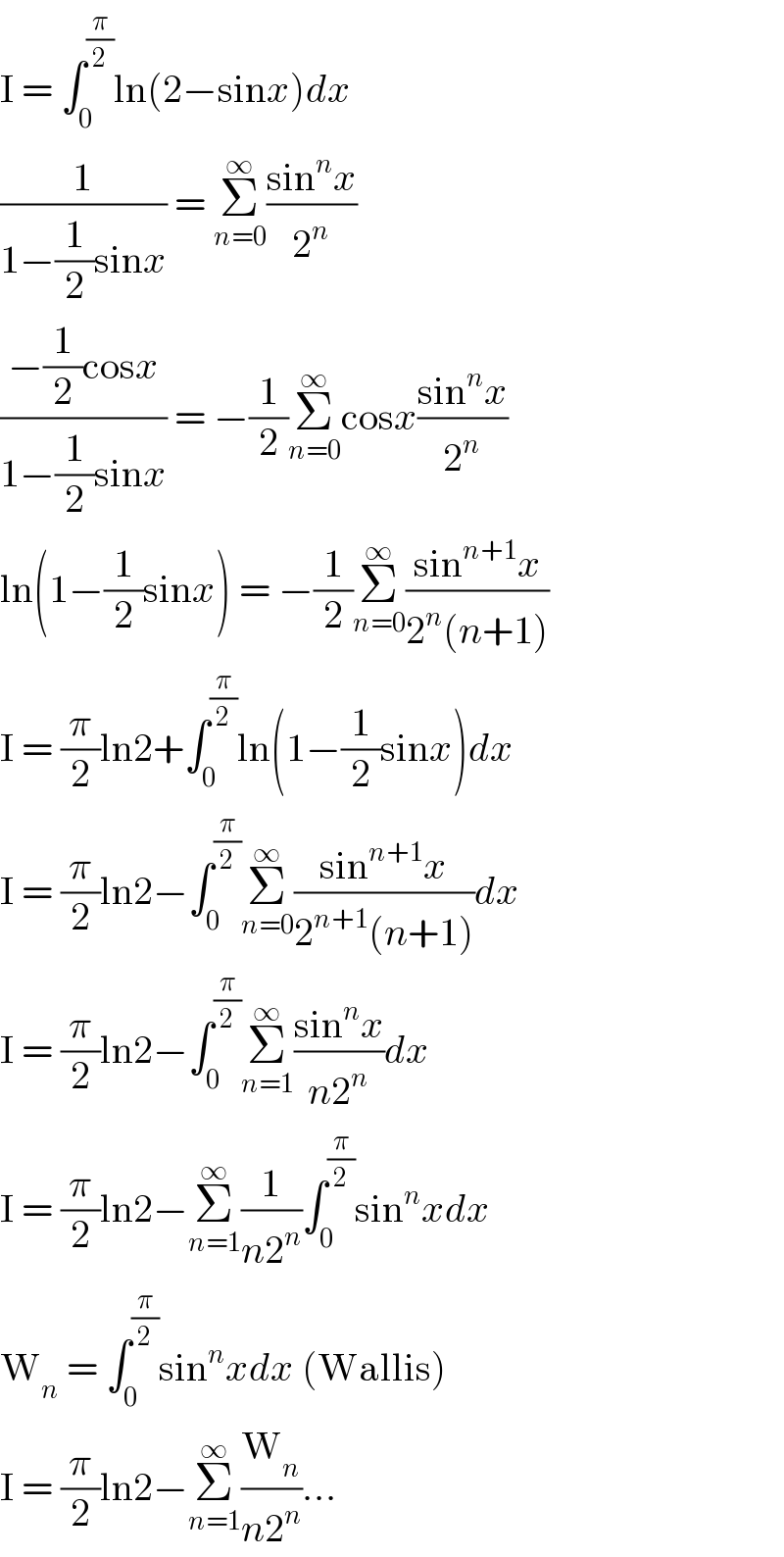
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2}−\mathrm{sin}{x}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}^{{n}} {x}}{\mathrm{2}^{{n}} } \\ $$$$\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}{x}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{cos}{x}\frac{\mathrm{sin}^{{n}} {x}}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}^{{n}+\mathrm{1}} {x}}{\mathrm{2}^{{n}} \left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{ln2}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}{x}\right){dx} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{ln2}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}^{{n}+\mathrm{1}} {x}}{\mathrm{2}^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)}{dx} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{ln2}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}^{{n}} {x}}{{n}\mathrm{2}^{{n}} }{dx} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{ln2}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\mathrm{2}^{{n}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{{n}} {xdx} \\ $$$$\mathrm{W}_{{n}} \:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{{n}} {xdx}\:\left(\mathrm{Wallis}\right) \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{ln2}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{W}_{{n}} }{{n}\mathrm{2}^{{n}} }... \\ $$
Answered by mathmax by abdo last updated on 15/Sep/20

$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2}−\mathrm{sinx}\right)\mathrm{dx}\:\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}\right)\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}\right)\mathrm{dx}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{1}−\mathrm{asinx}\right)\mathrm{dx} \\ $$$$\mathrm{with0}<\mathrm{a}<\mathrm{1} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{−\mathrm{sinx}}{\mathrm{1}−\mathrm{asinx}}\:\mathrm{dx}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{1}−\mathrm{a}\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}×\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{4t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\right)}\:\mathrm{dt}\:\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{tdt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}\right)} \\ $$$$\mathrm{let}\:\mathrm{decomoose}\:\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2at}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{a}^{\mathrm{2}} −\mathrm{1}<\mathrm{0}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\alpha\mathrm{t}\:+\beta}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}}\:+\frac{\mathrm{mt}\:+\mathrm{n}}{\mathrm{t}^{\mathrm{2}\:} \:+\mathrm{1}} \\ $$$$\Rightarrow\left(\alpha\mathrm{t}+\beta\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)+\left(\mathrm{mt}+\mathrm{n}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}\right)\:=\mathrm{t}\:\Rightarrow \\ $$$$\alpha\mathrm{t}^{\mathrm{3}} \:+\alpha\mathrm{t}\:+\beta\mathrm{t}^{\mathrm{2}} \:+\beta\:\:+\mathrm{mt}^{\mathrm{3}} −\mathrm{2amt}^{\mathrm{2}} +\mathrm{mt}\:+\mathrm{nt}^{\mathrm{2}} −\mathrm{2ant}\:+\mathrm{n}\:=\mathrm{t}\:\Rightarrow \\ $$$$\left(\alpha+\mathrm{m}\right)\mathrm{t}^{\mathrm{3}} \:+\left(\beta−\mathrm{2am}\:+\mathrm{n}\right)\mathrm{t}^{\mathrm{2}} \:+\left(\alpha+\mathrm{m}−\mathrm{2an}\right)\mathrm{t}\:+\beta+\mathrm{n}\:=\mathrm{t}\:\Rightarrow \\ $$$$\begin{cases}{\alpha+\mathrm{m}\:=\mathrm{0}}\\{\beta−\mathrm{2am}\:+\mathrm{n}\:=\mathrm{0}\:\:\:\:\mathrm{and}\:\begin{cases}{\alpha+\mathrm{m}\:−\mathrm{2an}\:=\mathrm{1}}\\{\beta+\mathrm{n}\:=\mathrm{0}\:\:\Rightarrow}\end{cases}}\end{cases} \\ $$$$\begin{cases}{\mathrm{m}=−\alpha\:\:\:\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\begin{cases}{−\mathrm{2an}\:=\mathrm{1}}\\{\beta\:=−\mathrm{n}\:\:\:\:\Rightarrow\:\mathrm{n}\:=−\frac{\mathrm{1}}{\mathrm{2a}}}\end{cases}}\\{−\mathrm{2a}\alpha\:=\mathrm{0}\:\:}\end{cases} \\ $$$$\mathrm{and}\:\alpha=\mathrm{0}\:\Rightarrow\mathrm{m}=\mathrm{0}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\frac{\mathrm{1}}{\mathrm{2a}}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}}\:+\frac{−\frac{\mathrm{1}}{\mathrm{2a}}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2a}}\left\{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\right\}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\frac{\mathrm{2}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}}\:+\frac{\mathrm{2}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{a}}×\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{2}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}}\:=\frac{\pi}{\mathrm{2a}}−\frac{\mathrm{2}}{\mathrm{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}} \\ $$$$\mathrm{but}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{1}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2at}\:+\mathrm{a}^{\mathrm{2}} +\mathrm{1}−\mathrm{a}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{a}\right)^{\mathrm{2}} \:+\mathrm{1}−\mathrm{a}^{\mathrm{2}} } \\ $$$$=_{\mathrm{t}−\mathrm{a}\:=\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }\mathrm{u}} \:\:\:\int_{\frac{−\mathrm{a}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}} ^{\frac{\mathrm{1}−\mathrm{a}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}} \:\:\:\:\:\:\frac{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}{\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\left\{\:\mathrm{arctan}\left(\frac{\mathrm{1}−\mathrm{a}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)+\mathrm{arctan}\left(\frac{\mathrm{a}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{2}}\mathrm{lna}\:\:−\mathrm{2}\:\int\:\:\frac{\mathrm{1}}{\mathrm{a}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\:\mathrm{arctan}\left(\frac{\mathrm{1}−\mathrm{a}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\mathrm{da}−\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{a}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\:\mathrm{arctan}\left(\frac{\mathrm{a}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\mathrm{da} \\ $$$$....\mathrm{be}\:\mathrm{continued}\:.... \\ $$
Commented by mathmax by abdo last updated on 16/Sep/20

$$\mathrm{we}\:\mathrm{have}\:\int\:\:\frac{\mathrm{1}}{\mathrm{a}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\:\mathrm{arctan}\left(\frac{\mathrm{1}−\mathrm{a}}{\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}\right)\mathrm{da} \\ $$$$=_{\mathrm{a}\:=\mathrm{cost}} \:\:\:\:\int\:\frac{\mathrm{1}}{\mathrm{cost}\:\mathrm{sint}}\:\mathrm{arctan}\left(\frac{\mathrm{1}−\mathrm{cost}}{\mathrm{sint}}\right)\left(−\mathrm{sint}\right)\mathrm{dt} \\ $$$$=−\int\:\:\frac{\mathrm{1}}{\mathrm{cost}}\:\mathrm{arctan}\left(\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)}{\mathrm{2sin}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}\right)\mathrm{dt} \\ $$$$=−\int\:\:\frac{\mathrm{1}}{\mathrm{cost}}\:\mathrm{arctan}\left(\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{\mathrm{t}}{\mathrm{cost}}\:\mathrm{dt}\right. \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{z}} \:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{\mathrm{2arctan}\left(\mathrm{z}\right)}{\frac{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }}\:\frac{\mathrm{2dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} } \\ $$$$=−\mathrm{2}\:\int\:\:\:\frac{\mathrm{arctan}\left(\mathrm{z}\right)}{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }\:\mathrm{dz}.....\mathrm{be}\:\mathrm{continued}... \\ $$
