Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 152420 by tabata last updated on 28/Aug/21

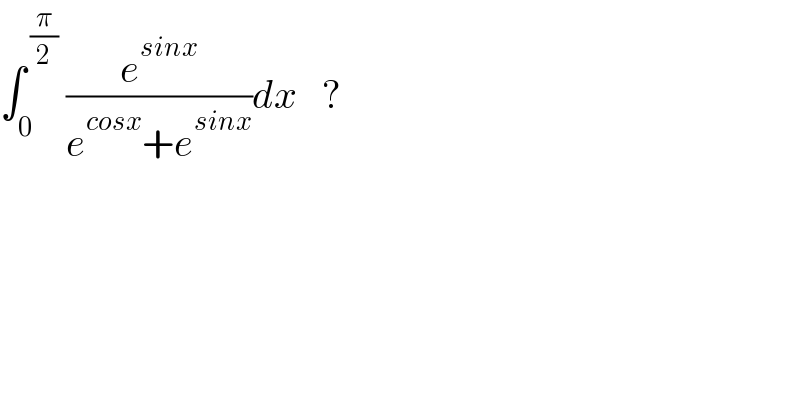
∫_0 ^( (π/2)) (e^(sinx) /(e^(cosx) +e^(sinx) ))dx ?

$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{{e}^{{sinx}} }{{e}^{{cosx}} +{e}^{{sinx}} }{dx}\:\:\:? \\ $$

Answered by mindispower last updated on 28/Aug/21

f(a+b−x)+f(x)=c ∫_a ^b f(x)dx=(1/2)c(b−a)

$${f}\left({a}+{b}−{x}\right)+{f}\left({x}\right)={c} \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}{c}\left({b}−{a}\right) \\ $$

Answered by Lordose last updated on 28/Aug/21

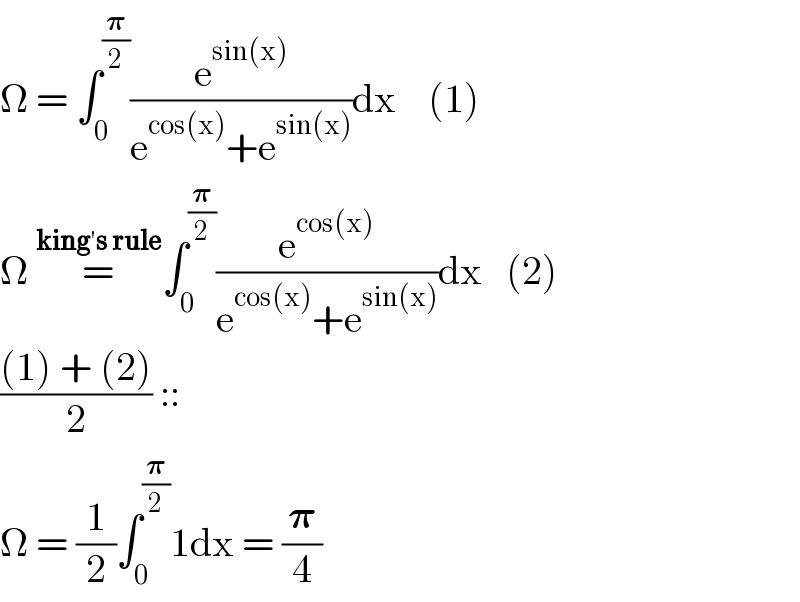
Ω = ∫_0 ^(𝛑/2) (e^(sin(x)) /(e^(cos(x)) +e^(sin(x)) ))dx (1) Ω =^(king′s rule) ∫_0 ^(𝛑/2) (e^(cos(x)) /(e^(cos(x)) +e^(sin(x)) ))dx (2) (((1) + (2))/2) :: Ω = (1/2)∫_0 ^(𝛑/2) 1dx = (𝛑/4)

$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\mathrm{e}^{\mathrm{sin}\left(\mathrm{x}\right)} }{\mathrm{e}^{\mathrm{cos}\left(\mathrm{x}\right)} +\mathrm{e}^{\mathrm{sin}\left(\mathrm{x}\right)} }\mathrm{dx}\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\Omega\:\overset{\boldsymbol{\mathrm{king}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{rule}}} {=}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\mathrm{e}^{\mathrm{cos}\left(\mathrm{x}\right)} }{\mathrm{e}^{\mathrm{cos}\left(\mathrm{x}\right)} +\mathrm{e}^{\mathrm{sin}\left(\mathrm{x}\right)} }\mathrm{dx}\:\:\:\left(\mathrm{2}\right) \\ $$$$\frac{\left(\mathrm{1}\right)\:+\:\left(\mathrm{2}\right)}{\mathrm{2}}\::: \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \mathrm{1dx}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com