
Question Number 117216 by bobhans last updated on 10/Oct/20
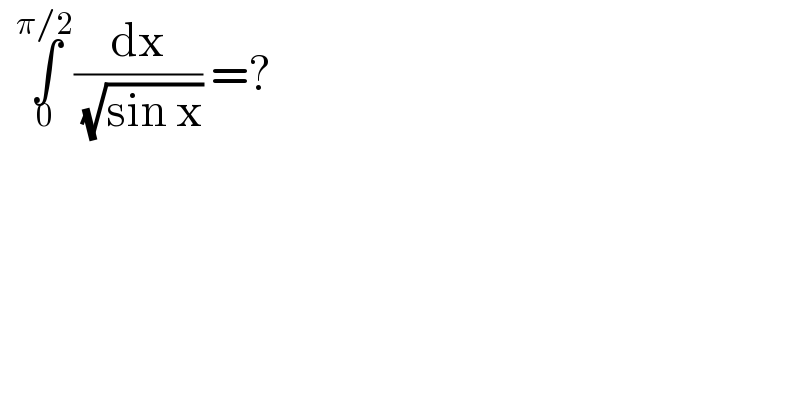
$$\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{dx}}{\:\sqrt{\mathrm{sin}\:\mathrm{x}}}\:=?\: \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 10/Oct/20
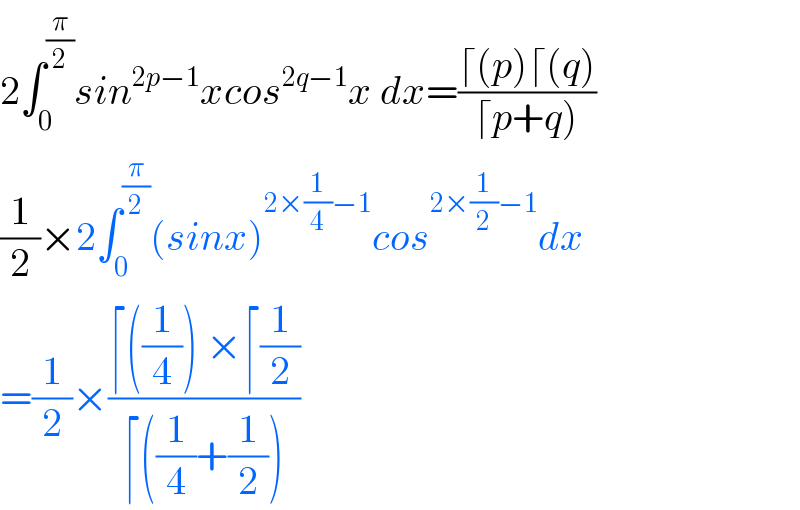
$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{p}−\mathrm{1}} {xcos}^{\mathrm{2}{q}−\mathrm{1}} {x}\:{dx}=\frac{\lceil\left({p}\right)\lceil\left({q}\right)}{\left.\lceil{p}+{q}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sinx}\right)^{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} {cos}^{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:×\lceil\frac{\mathrm{1}}{\mathrm{2}}}{\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:\: \\ $$
Commented by bobhans last updated on 10/Oct/20

$$\mathrm{this}\:\mathrm{is}\:\Gamma\:=\:\:\mathrm{gamma}\:\mathrm{function}? \\ $$
Commented by TANMAY PANACEA last updated on 10/Oct/20

$${yes}\:{sir} \\ $$
Commented by bobhans last updated on 10/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
