Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 197436 by horsebrand11 last updated on 17/Sep/23

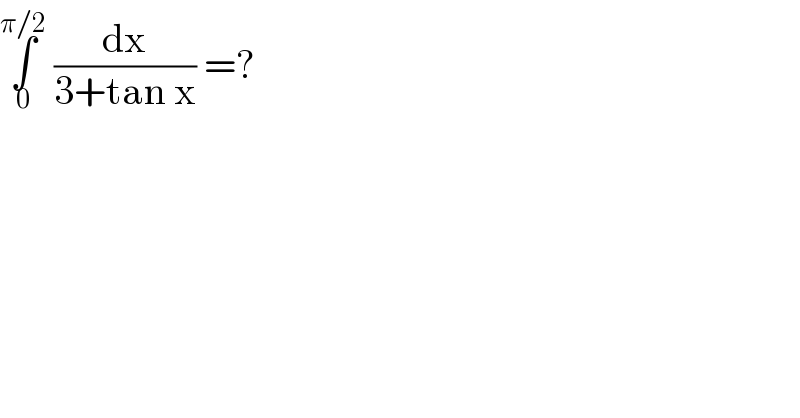
∫_0 ^(π/2) (dx/(3+tan x)) =?

$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{dx}}{\mathrm{3}+\mathrm{tan}\:\mathrm{x}}\:=? \\ $$

Answered by Frix last updated on 17/Sep/23

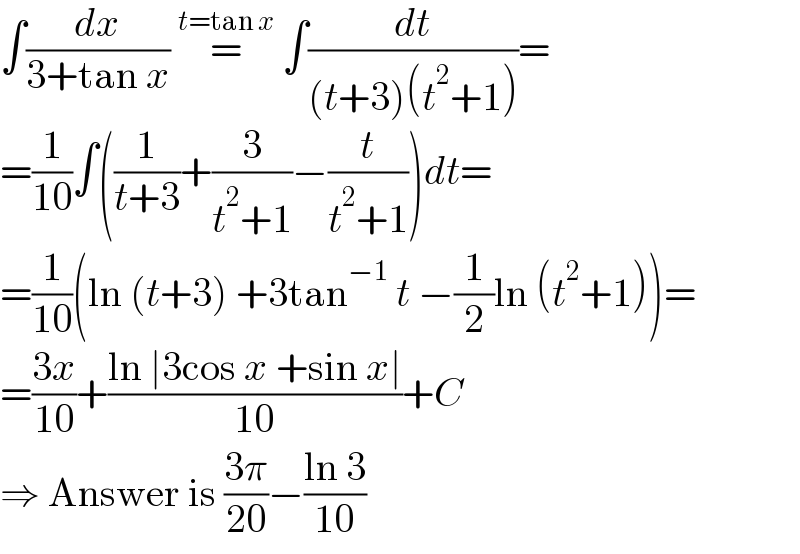
∫(dx/(3+tan x)) =^(t=tan x) ∫(dt/((t+3)(t^2 +1)))= =(1/(10))∫((1/(t+3))+(3/(t^2 +1))−(t/(t^2 +1)))dt= =(1/(10))(ln (t+3) +3tan^(−1) t −(1/2)ln (t^2 +1))= =((3x)/(10))+((ln ∣3cos x +sin x∣)/(10))+C ⇒ Answer is ((3π)/(20))−((ln 3)/(10))

$$\int\frac{{dx}}{\mathrm{3}+\mathrm{tan}\:{x}}\:\overset{{t}=\mathrm{tan}\:{x}} {=}\:\int\frac{{dt}}{\left({t}+\mathrm{3}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\int\left(\frac{\mathrm{1}}{{t}+\mathrm{3}}+\frac{\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{ln}\:\left({t}+\mathrm{3}\right)\:+\mathrm{3tan}^{−\mathrm{1}} \:{t}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\right)= \\ $$$$=\frac{\mathrm{3}{x}}{\mathrm{10}}+\frac{\mathrm{ln}\:\mid\mathrm{3cos}\:{x}\:+\mathrm{sin}\:{x}\mid}{\mathrm{10}}+{C} \\ $$$$\Rightarrow\:\mathrm{Answer}\:\mathrm{is}\:\frac{\mathrm{3}\pi}{\mathrm{20}}−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{10}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com