
Question Number 160597 by cortano last updated on 03/Dec/21
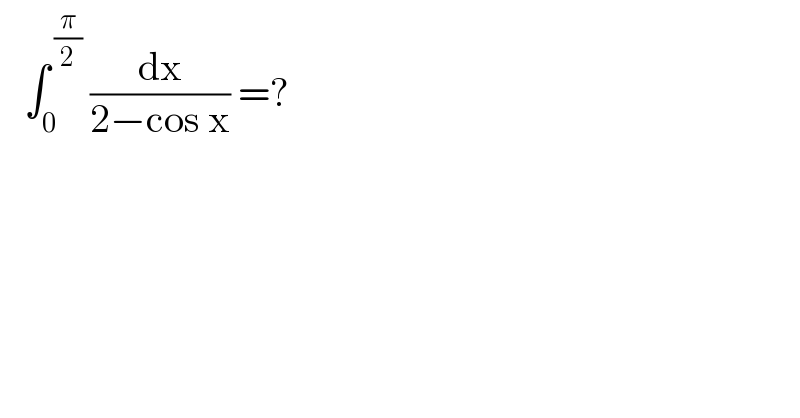
$$\:\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{2}−\mathrm{cos}\:\mathrm{x}}\:=? \\ $$
Answered by Mathspace last updated on 03/Dec/21
![I=∫_0 ^(π/2) (dx/(2−cosx)) we do the changement tan((x/2))=t ⇒I=∫_0 ^1 ((2dt)/((1+t^2 )(2−((1−t^2 )/(1+t^2 ))))) =2∫_0 ^1 (dt/(2+2t^2 −1+t^2 ))=2∫_0 ^1 (dt/(3t^2 +1)) =_((√3)t=u) 2∫_0 ^(√3) (du/( (√3)(1+u^2 ))) =(2/( (√3)))[arctanu]_0 ^(√3) =(2/( (√3)))arctan((√3))](Q160598.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{2}−{cosx}}\:{we}\:{do}\:{the}\:{changement} \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:\Rightarrow{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{2}−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}+{t}^{\mathrm{2}} }=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=_{\sqrt{\mathrm{3}}{t}={u}} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{du}}{\:\sqrt{\mathrm{3}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left[{arctanu}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\sqrt{\mathrm{3}}\right) \\ $$
Commented by cortano last updated on 03/Dec/21

$$\mathrm{yes}.... \\ $$
