Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 218709 by Nicholas666 last updated on 14/Apr/25

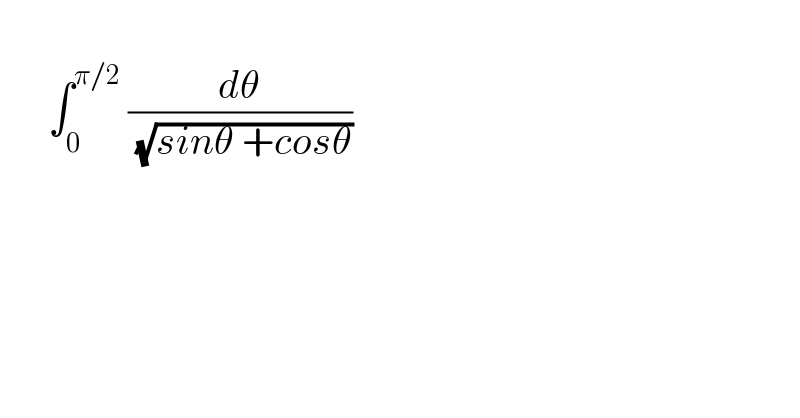
∫_0 ^(π/2) (dθ/( (√(sinθ +cosθ))))

$$ \\ $$$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{{d}\theta}{\:\sqrt{{sin}\theta\:+{cos}\theta}} \\ $$$$ \\ $$

Answered by Nicholas666 last updated on 14/Apr/25

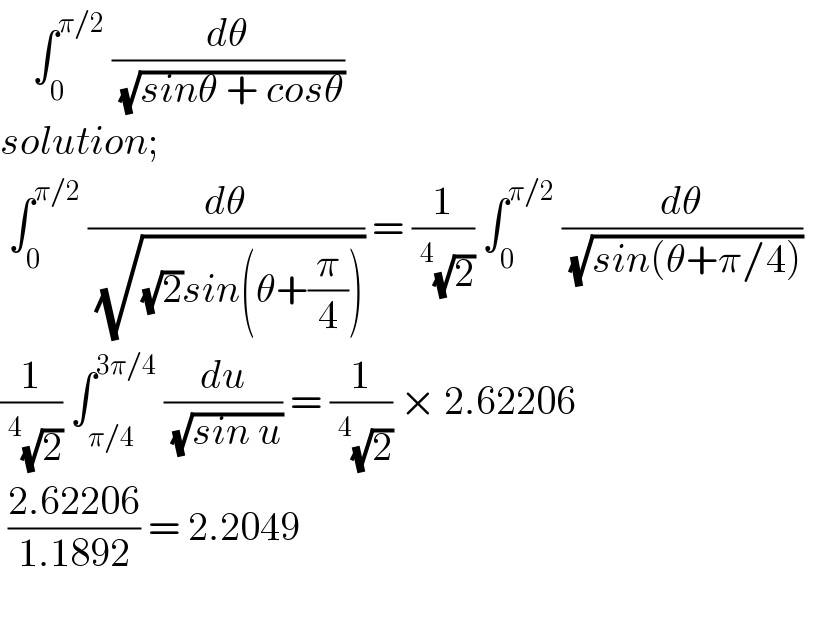
∫_0 ^(π/2) (dθ/( (√(sinθ + cosθ)))) solution; ∫_0 ^(π/2) (dθ/( (√((√2)sin(θ+(π/4)))))) = (1/(^4 (√2))) ∫_0 ^(π/2) (dθ/( (√(sin(θ+π/4))))) (1/(^4 (√2))) ∫_(π/4) ^(3π/4) (du/( (√(sin u)))) = (1/(^4 (√2))) × 2.62206 ((2.62206)/(1.1892)) = 2.2049

$$\:\:\:\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{{d}\theta}{\:\sqrt{{sin}\theta\:+\:{cos}\theta}} \\ $$$${solution}; \\ $$$$\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{{d}\theta}{\:\sqrt{\sqrt{\mathrm{2}}{sin}\left(\theta+\frac{\pi}{\mathrm{4}}\right)}}\:=\:\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\frac{{d}\theta}{\:\sqrt{{sin}\left(\theta+\pi/\mathrm{4}\right)}}\:\: \\ $$$$\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{2}}}\:\int_{\pi/\mathrm{4}} ^{\mathrm{3}\pi/\mathrm{4}} \:\frac{{du}}{\:\sqrt{{sin}\:{u}}}\:=\:\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{2}}}\:×\:\mathrm{2}.\mathrm{62206}\: \\ $$$$\:\frac{\mathrm{2}.\mathrm{62206}}{\mathrm{1}.\mathrm{1892}}\:=\:\mathrm{2}.\mathrm{2049} \\ $$$$\: \\ $$

Answered by Ghisom last updated on 14/Apr/25

∫_0 ^(π/2) (dθ/( (√(cos θ +sin θ))))=2∫_(π/4) ^(π/2) (dθ/( (√(cos θ +sin θ))))= [t=(x/2)−(π/8)] =2^(7/4) ∫_0 ^(π/8) (dt/( (√(1−2sin^2 t))))=2^(7/4) [F (t∣2)]_0 ^(π/8) = =2^(7/4) F ((π/8)∣2) ≈1.39739529927

$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{d}\theta}{\:\sqrt{\mathrm{cos}\:\theta\:+\mathrm{sin}\:\theta}}=\mathrm{2}\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{d}\theta}{\:\sqrt{\mathrm{cos}\:\theta\:+\mathrm{sin}\:\theta}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{8}}\right] \\ $$$$=\mathrm{2}^{\mathrm{7}/\mathrm{4}} \underset{\mathrm{0}} {\overset{\pi/\mathrm{8}} {\int}}\frac{{dt}}{\:\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:{t}}}=\mathrm{2}^{\mathrm{7}/\mathrm{4}} \left[\mathrm{F}\:\left({t}\mid\mathrm{2}\right)\right]_{\mathrm{0}} ^{\pi/\mathrm{8}} = \\ $$$$=\mathrm{2}^{\mathrm{7}/\mathrm{4}} \mathrm{F}\:\left(\frac{\pi}{\mathrm{8}}\mid\mathrm{2}\right)\:\approx\mathrm{1}.\mathrm{39739529927} \\ $$

Commented by Nicholas666 last updated on 16/Apr/25

thank you for your solution

$${thank}\:{you}\:{for}\:{your}\:{solution} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com