
Question Number 83146 by 09658867628 last updated on 28/Feb/20
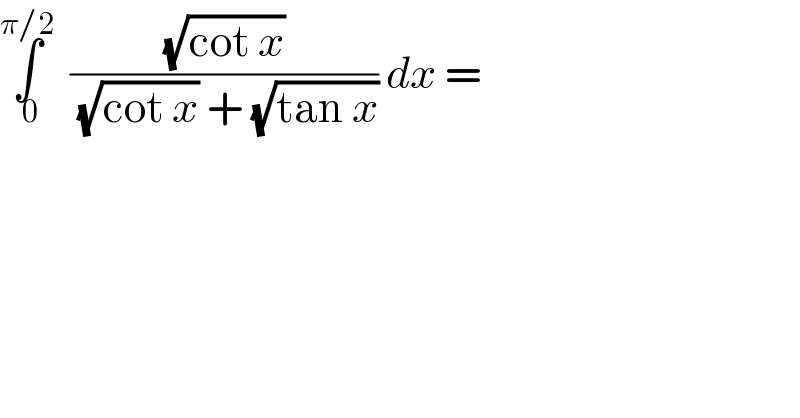
$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\:\frac{\sqrt{\mathrm{cot}\:{x}}}{\sqrt{\mathrm{cot}\:{x}}\:+\:\sqrt{\mathrm{tan}\:{x}}}\:{dx}\:= \\ $$
Answered by Kunal12588 last updated on 28/Feb/20
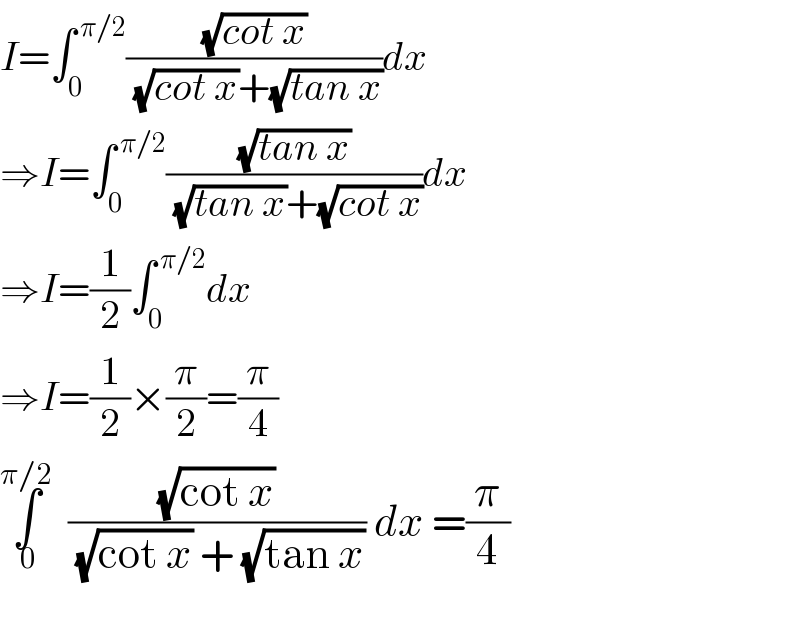
$${I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\sqrt{{cot}\:{x}}}{\sqrt{{cot}\:{x}}+\sqrt{{tan}\:{x}}}{dx} \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\sqrt{{tan}\:{x}}}{\sqrt{{tan}\:{x}}+\sqrt{{cot}\:{x}}}{dx} \\ $$$$\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} {dx} \\ $$$$\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\:\frac{\sqrt{\mathrm{cot}\:{x}}}{\sqrt{\mathrm{cot}\:{x}}\:+\:\sqrt{\mathrm{tan}\:{x}}}\:{dx}\:=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Answered by niroj last updated on 28/Feb/20
![let, I= ∫_0 ^(π/2) (( (√(cot x)))/( (√(cot x)) +(√(tan x))))dx.....(i) = ∫_0 ^(π/2) ((√( cot ((π/2)−x)))/( (√(cot ((π/2))) −x)+ (√(tan ((π/2) −x)))))dx ∵ ∫_0 ^( a) xdx=∫_0 ^a (a−x)dx = ∫_0 ^( (π/2)) ((√(tan x))/( (√(tan x)) +(√(cot x))))dx......(ii) added (i)&(ii) 2I= ∫_0 ^(π/2) ( (( (√(cot x)))/( (√(cot x)) +(√(tan x)))) + ((√(tan x))/( (√(tan x)) +(√(cot x)))))dx 2I= ∫_0 ^( (π/2)) ((( (√(cot x)) +(√(tan x)))/( (√(cot x))+(√(tan x)))))dx 2I= ∫_0 ^(π/2) dx 2I= [ x]_0 ^(π/2) 2I= ((π/2)−0) 2I= (π/2) ⇒ I= (π/4) //.](Q83151.png)
$$\:\mathrm{let},\:\mathrm{I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\:\sqrt{\mathrm{cot}\:\mathrm{x}}}{\:\sqrt{\mathrm{cot}\:\mathrm{x}}\:+\sqrt{\mathrm{tan}\:\mathrm{x}}}\mathrm{dx}.....\left(\mathrm{i}\right) \\ $$$$\:\:\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\sqrt{\:\mathrm{cot}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}}{\left.\:\sqrt{\mathrm{cot}\:\left(\frac{\pi}{\mathrm{2}}\right.}\:−\mathrm{x}\right)+\:\sqrt{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}\:−\mathrm{x}\right)}}\mathrm{dx}\:\:\:\:\:\because\:\int_{\mathrm{0}} ^{\:\mathrm{a}} \mathrm{xdx}=\int_{\mathrm{0}} ^{\mathrm{a}} \left(\mathrm{a}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\sqrt{\mathrm{tan}\:\mathrm{x}}}{\:\sqrt{\mathrm{tan}\:\mathrm{x}}\:+\sqrt{\mathrm{cot}\:\mathrm{x}}}\mathrm{dx}......\left(\mathrm{ii}\right) \\ $$$$\:\:\mathrm{added}\:\left(\mathrm{i}\right)\&\left(\mathrm{ii}\right) \\ $$$$\:\:\mathrm{2I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\:\frac{\:\:\:\sqrt{\mathrm{cot}\:\mathrm{x}}}{\:\sqrt{\mathrm{cot}\:\mathrm{x}}\:\:+\sqrt{\mathrm{tan}\:\mathrm{x}}}\:+\:\frac{\sqrt{\mathrm{tan}\:\mathrm{x}}}{\:\:\sqrt{\mathrm{tan}\:\mathrm{x}}\:+\sqrt{\mathrm{cot}\:\mathrm{x}}}\right)\mathrm{dx} \\ $$$$\:\:\mathrm{2I}=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\:\left(\frac{\:\:\sqrt{\mathrm{cot}\:\mathrm{x}}\:\:+\sqrt{\mathrm{tan}\:\mathrm{x}}}{\:\:\sqrt{\mathrm{cot}\:\mathrm{x}}+\sqrt{\mathrm{tan}\:\mathrm{x}}}\right)\mathrm{dx} \\ $$$$\:\:\mathrm{2I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{dx} \\ $$$$\:\:\mathrm{2I}=\:\left[\:\mathrm{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:\mathrm{2I}=\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{0}\right) \\ $$$$\:\:\:\:\mathrm{2I}=\:\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\mathrm{I}=\:\frac{\pi}{\mathrm{4}}\://. \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 28/Feb/20
$${thank}\:{you}\:{both} \\ $$
