
Question Number 221048 by fantastic last updated on 23/May/25
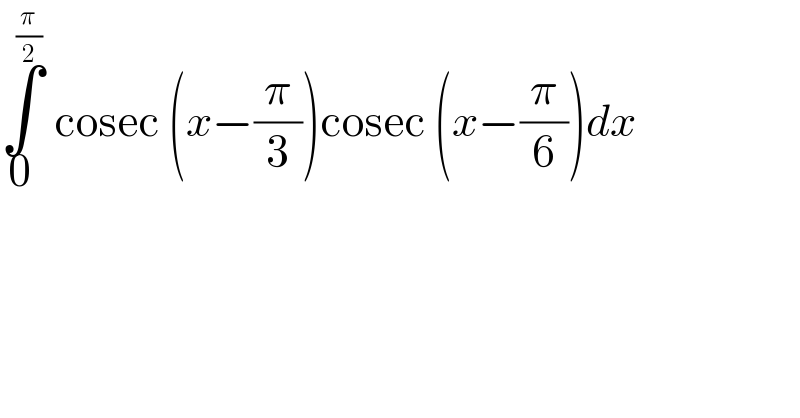
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{cosec}\:\left({x}−\frac{\pi}{\mathrm{3}}\right)\mathrm{cosec}\:\left({x}−\frac{\pi}{\mathrm{6}}\right){dx}\: \\ $$
Answered by vnm last updated on 24/May/25
![the integral diverges, but it′s possible to calculate its p.v. ∫(dx/(sin(x−(π/3))sin(x−(π/6))))= ∫(dx/((1/2)(cos(−(π/6))−cos(2x−(π/2)))))= ∫((2dx)/(((√3)/2)−sin2x))=[tgx=u]= ∫((2du)/(1+u^2 ))∙(1/( ((√3)/2)−((2u)/(1+u^2 ))))=∫((2du)/(((√3)/2)u^2 −2u+((√3)/2)))=(4/( (√3)))∫(du/(u^2 −(4/( (√3)))u+1))= (4/( (√3)))∫(du/((u−(2/( (√3))))^2 −((1/( (√3))))^2 ))=(4/( (√3)))∙(1/(2(1/( (√3)))))∫((1/(u−(√3)))−(1/(u−(1/( (√3))))))du= 2ln∣((u−(√3))/(u−1/(√3)))∣+C=2ln∣((tgx−(√3))/(tgx−(1/( (√3)))))∣+C let f(x)=(1/(sin(x−(π/3))sin(x−(π/6)))) lim_(ε→+0) (∫_0 ^((π/6)−ε) f(x)dx+∫_((π/6)+ε) ^((π/3)−ε) f(x)dx+∫_((π/3)+ε) ^(π/2) f(x)dx)≈−2ln 3 the result is obtained by numeircal integration [2ln∣((tgx−(√3))/(tgx−1/(√3)))∣]_0 ^(π/2) =2(ln 1−ln 3)=−2ln 3 As I said the integral diverges, −2ln 3 being its prime value.](Q221061.png)
$$ \\ $$$$\mathrm{the}\:\mathrm{integral}\:\mathrm{diverges},\:\mathrm{but}\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{possible}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{its}\:\mathrm{p}.\mathrm{v}. \\ $$$$\int\frac{{dx}}{\mathrm{sin}\left({x}−\frac{\pi}{\mathrm{3}}\right)\mathrm{sin}\left({x}−\frac{\pi}{\mathrm{6}}\right)}= \\ $$$$\int\frac{{dx}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\left(−\frac{\pi}{\mathrm{6}}\right)−\mathrm{cos}\left(\mathrm{2}{x}−\frac{\pi}{\mathrm{2}}\right)\right)}= \\ $$$$\int\frac{\mathrm{2}{dx}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{sin2}{x}}=\left[\mathrm{tg}{x}={u}\right]= \\ $$$$\int\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}=\int\frac{\mathrm{2}{du}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}^{\mathrm{2}} −\mathrm{2}{u}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\int\frac{{du}}{{u}^{\mathrm{2}} −\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}{u}+\mathrm{1}}= \\ $$$$\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\int\frac{{du}}{\left({u}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\centerdot\frac{\mathrm{1}}{\mathrm{2}\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\int\left(\frac{\mathrm{1}}{{u}−\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{{u}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\right){du}= \\ $$$$\mathrm{2ln}\mid\frac{{u}−\sqrt{\mathrm{3}}}{{u}−\mathrm{1}/\sqrt{\mathrm{3}}}\mid+{C}=\mathrm{2ln}\mid\frac{\mathrm{tg}{x}−\sqrt{\mathrm{3}}}{\mathrm{tg}{x}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\mid+{C} \\ $$$$\mathrm{let}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{sin}\left({x}−\frac{\pi}{\mathrm{3}}\right)\mathrm{sin}\left({x}−\frac{\pi}{\mathrm{6}}\right)} \\ $$$$\underset{\varepsilon\rightarrow+\mathrm{0}} {\mathrm{lim}}\left(\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}−\varepsilon} {f}\left({x}\right){dx}+\int_{\frac{\pi}{\mathrm{6}}+\varepsilon} ^{\frac{\pi}{\mathrm{3}}−\varepsilon} {f}\left({x}\right){dx}+\int_{\frac{\pi}{\mathrm{3}}+\varepsilon} ^{\frac{\pi}{\mathrm{2}}} {f}\left({x}\right){dx}\right)\approx−\mathrm{2ln}\:\mathrm{3} \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{obtained}\:\mathrm{by}\:\mathrm{numeircal}\:\mathrm{integration} \\ $$$$\left[\mathrm{2ln}\mid\frac{\mathrm{tg}{x}−\sqrt{\mathrm{3}}}{\mathrm{tg}{x}−\mathrm{1}/\sqrt{\mathrm{3}}}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{2}\left(\mathrm{ln}\:\mathrm{1}−\mathrm{ln}\:\mathrm{3}\right)=−\mathrm{2ln}\:\mathrm{3} \\ $$$$ \\ $$$$\mathrm{As}\:\mathrm{I}\:\mathrm{said}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{diverges},\: \\ $$$$−\mathrm{2ln}\:\mathrm{3}\:\mathrm{being}\:\mathrm{its}\:\mathrm{prime}\:\mathrm{value}. \\ $$
Answered by Frix last updated on 24/May/25
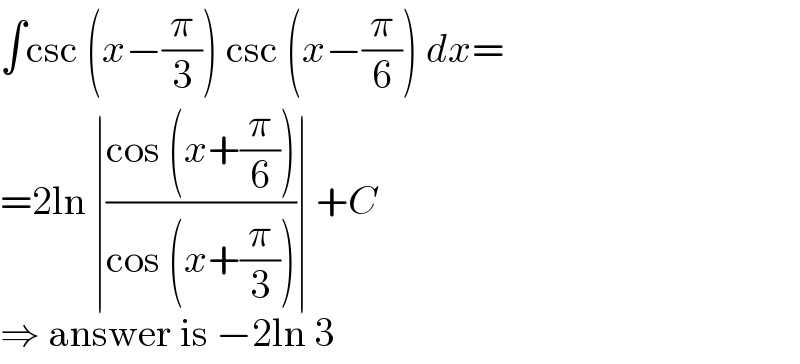
$$\int\mathrm{csc}\:\left({x}−\frac{\pi}{\mathrm{3}}\right)\:\mathrm{csc}\:\left({x}−\frac{\pi}{\mathrm{6}}\right)\:{dx}= \\ $$$$=\mathrm{2ln}\:\mid\frac{\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{6}}\right)}{\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{3}}\right)}\mid\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:−\mathrm{2ln}\:\mathrm{3} \\ $$
