
Question Number 167328 by cortano1 last updated on 13/Mar/22
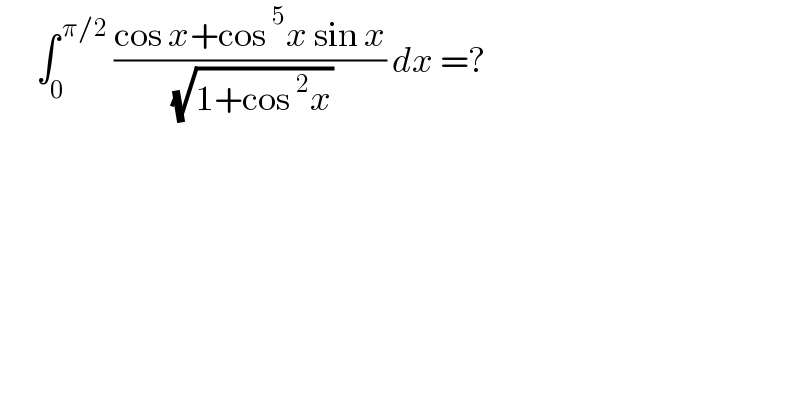
$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{cos}\:{x}+\mathrm{cos}\:^{\mathrm{5}} {x}\:\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}}\:{dx}\:=? \\ $$
Answered by MJS_new last updated on 13/Mar/22
![∫((cos x +cos^5 x sin x)/( (√(1+cos^2 x))))dx= [t=arcsin ((sin x)/( (√2))) → dx=((√(1+cos^2 x))/(cos x))dt] = ... =((√2)/4)∫(sin 5t −sin 3t +2sin t +3(√2))dt= =−((√2)/(20))cos 5t +((√2)/(12))cos 3t −((√2)/2)cos t +t= ... =arcsin ((sin x)/( (√2))) −((√(1+cos^2 x))/(15))(3cos^4 x −4cos^2 x +8)+C](Q167345.png)
$$\int\frac{\mathrm{cos}\:{x}\:+\mathrm{cos}^{\mathrm{5}} \:{x}\:\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{2}}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}}{\mathrm{cos}\:{x}}{dt}\right] \\ $$$$= \\ $$$$... \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\left(\mathrm{sin}\:\mathrm{5}{t}\:−\mathrm{sin}\:\mathrm{3}{t}\:+\mathrm{2sin}\:{t}\:+\mathrm{3}\sqrt{\mathrm{2}}\right){dt}= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{20}}\mathrm{cos}\:\mathrm{5}{t}\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\mathrm{cos}\:\mathrm{3}{t}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{cos}\:{t}\:+{t}= \\ $$$$... \\ $$$$=\mathrm{arcsin}\:\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{2}}}\:−\frac{\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}}{\mathrm{15}}\left(\mathrm{3cos}^{\mathrm{4}} \:{x}\:−\mathrm{4cos}^{\mathrm{2}} \:{x}\:+\mathrm{8}\right)+{C} \\ $$
