
Question Number 139414 by mathdanisur last updated on 26/Apr/21
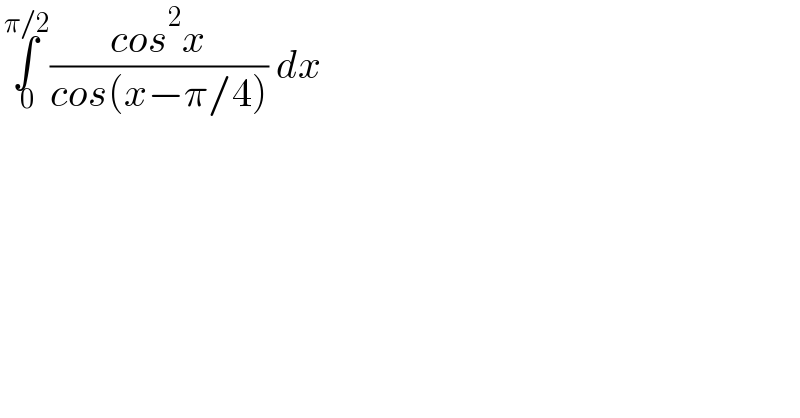
$$\underset{\:\mathrm{0}} {\overset{\:\pi/\mathrm{2}} {\int}}\frac{{cos}^{\mathrm{2}} {x}}{{cos}\left({x}−\pi/\mathrm{4}\right)}\:{dx} \\ $$
Commented by mr W last updated on 27/Apr/21
![(1/2)[ln ((1+sin (x−(π/4)))/(1−sin (x−(π/4))))]_0 ^(π/2) =(1/2)ln ((1+((√2)/2))/(1−((√2)/2)))=ln (1+(√2))](Q139448.png)
$$\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\:\frac{\mathrm{1}+\mathrm{sin}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{1}−\mathrm{sin}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}=\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
Answered by Ar Brandon last updated on 27/Apr/21
![=∫_0 ^(π/2) ((cos^2 x)/(cos(x−(π/4))))dx...(1), u=(π/2)−x =∫_0 ^(π/2) ((sin^2 x)/(cos((π/4)−x)))dx=∫_0 ^(π/2) ((sin^2 x)/(cos(x−(π/4))))dx...(2) (1)+(2) =(1/2)∫_0 ^(π/2) ((cos^2 x+sin^2 x)/(cos(x−(π/4))))dx=(1/2)∫_0 ^(π/2) (dx/(cos(x−(π/4)))) =(1/2)[ln∣sec(x−(π/4))+tan(x−(π/4))∣]_0 ^(π/2) =(1/2)[ln∣sec((π/4))+tan((π/4))∣−ln∣sec(−(π/4))+tan(−(π/4))∣] =(1/2)[ln∣(√2)+1∣−ln∣(√2)−1∣]=(1/2)ln∣(((√2)+1)/( (√2)−1))∣=ln((√2)+1)](Q139491.png)
$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)}\mathrm{dx}...\left(\mathrm{1}\right),\:\mathrm{u}=\frac{\pi}{\mathrm{2}}−\mathrm{x} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)}\mathrm{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)}\mathrm{dx}...\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{cos}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\mid\mathrm{sec}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\mid\mathrm{sec}\left(\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}\right)\mid−\mathrm{ln}\mid\mathrm{sec}\left(−\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\left(−\frac{\pi}{\mathrm{4}}\right)\mid\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\mid\sqrt{\mathrm{2}}+\mathrm{1}\mid−\mathrm{ln}\mid\sqrt{\mathrm{2}}−\mathrm{1}\mid\right]=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\mid=\mathrm{ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$
Commented by mathdanisur last updated on 30/Apr/21

$${thankyou}\:{sir} \\ $$
