
Question Number 221360 by Nicholas666 last updated on 31/May/25
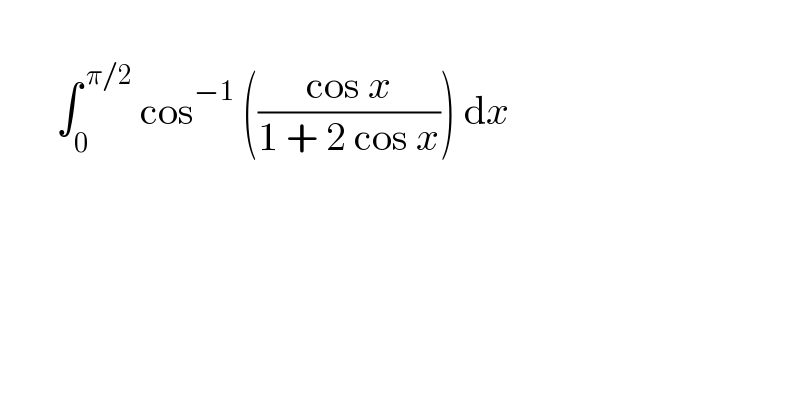
$$ \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\mathrm{cos}^{−\mathrm{1}} \:\left(\frac{\mathrm{cos}\:{x}}{\mathrm{1}\:+\:\mathrm{2}\:\mathrm{cos}\:{x}}\right)\:\mathrm{d}{x} \\ $$$$ \\ $$
Answered by MrGaster last updated on 06/Jun/25
![t=tan((x/2))⇒dx=(2/(1+t^2 ))dt,cos x=((1−t^2 )/(1+t^2 )) x=0⇒t=0,x=(π/2)⇒t=1 ((cos x)/(1+2 cos x))=(((1−t^2 )/(1+t^2 ))/(1+2((1−t^2 )/(1+t^2 ))))=(((1−t^2 )/(1+t^2 ))/((1+t^2 +2(1−t^2 ))/(1+t^2 )))=((1−t^2 )/(3−t^2 )) cos^(−1) (((cos x)/(1+2 cos x)))=cos^(−1) (((1−t^2 )/(3−t^2 ))) ∫_0 ^(π/2) cos^(−1) (((cos x)/(1+2 cos x)))dx=∫_0 ^1 cos^(−1) (((1−t^2 )/(3−t^2 )))(2/(1+t^2 ))dt u=arctan⇒t=tan u,dt=(du/(1+t^2 )),u∈[0,(π/4)] ∫_0 ^1 cos^(−1) (((1−t^2 )/(3−t^2 )))(2/(1+t^2 ))dt=2∫_0 ^(π/4) cos^(−1) (((1−tan^2 u)/(3−tan^2 u)))du ((1−tan^2 u)/(3−tan^2 u))=(((cos 2u)/(cos^2 u))/((3 cos^2 u−sin^2 u)/(cso^2 u)))=((cos 2u)/(3 cos^2 u−sin^2 u))=((cos 2u)/(1+2 cos 2u)) 2∫_0 ^(π/4) cos^(−1) (((cos 2u)/(1+2 cos 2u)))du u=2u⇒dv=2du,u=0⇒v=0 2∫_0 ^(π/4) cos^(−1) (((cos 2u)/(1+2 cos 2u)))du=∫_0 ^(π/2) cos^(−1) (((cos u)/(1+2 cos v)))dv ∫_0 ^(π/2) cos^(−1) (((cos v)/(1+2 cos v)))dv_(I) Γ(s)=∫_0 ^∞ t^(s−1) e^(−t) dt,ζ(s)=Σ_(n=1) ^∞ (1/n^s ) I=((5π^2 )/(24))](Q221485.png)
$${t}=\mathrm{tan}\left(\frac{{x}}{\mathrm{2}}\right)\Rightarrow{dx}=\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt},\mathrm{cos}\:{x}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${x}=\mathrm{0}\Rightarrow{t}=\mathrm{0},{x}=\frac{\pi}{\mathrm{2}}\Rightarrow{t}=\mathrm{1} \\ $$$$\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:{x}}=\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{2}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}=\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{3}−{t}^{\mathrm{2}} } \\ $$$$\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:{x}}\right)=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{3}−{t}^{\mathrm{2}} }\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:{x}}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{3}−{t}^{\mathrm{2}} }\right)\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${u}=\mathrm{arctan}\Rightarrow{t}=\mathrm{tan}\:{u},{dt}=\frac{{du}}{\mathrm{1}+{t}^{\mathrm{2}} },{u}\in\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\right] \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{3}−{t}^{\mathrm{2}} }\right)\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {u}}{\mathrm{3}−\mathrm{tan}^{\mathrm{2}} {u}}\right){du} \\ $$$$\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} {u}}{\mathrm{3}−\mathrm{tan}^{\mathrm{2}} {u}}=\frac{\frac{\mathrm{cos}\:\mathrm{2}{u}}{\mathrm{cos}^{\mathrm{2}} {u}}}{\frac{\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} {u}−\mathrm{sin}^{\mathrm{2}} {u}}{\mathrm{cso}^{\mathrm{2}} {u}}}=\frac{\mathrm{cos}\:\mathrm{2}{u}}{\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} {u}−\mathrm{sin}^{\mathrm{2}} {u}}=\frac{\mathrm{cos}\:\mathrm{2}{u}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}{u}} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\mathrm{2}{u}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}{u}}\right){du} \\ $$$${u}=\mathrm{2}{u}\Rightarrow{dv}=\mathrm{2}{du},{u}=\mathrm{0}\Rightarrow{v}=\mathrm{0} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\mathrm{2}{u}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}{u}}\right){du}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:{u}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:{v}}\right){dv} \\ $$$$\underset{{I}} {\underbrace{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:{v}}{\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:{v}}\right){dv}}} \\ $$$$\Gamma\left({s}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{s}−\mathrm{1}} {e}^{−{t}} {dt},\zeta\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} } \\ $$$${I}=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$
