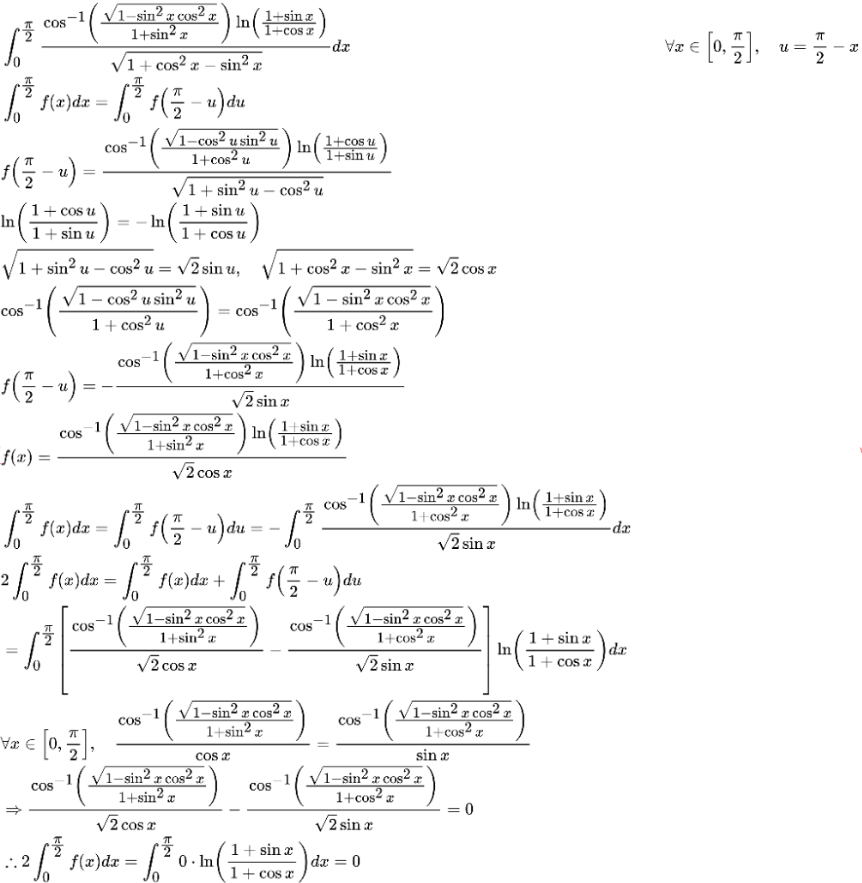Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 222245 by Nicholas666 last updated on 20/Jun/25

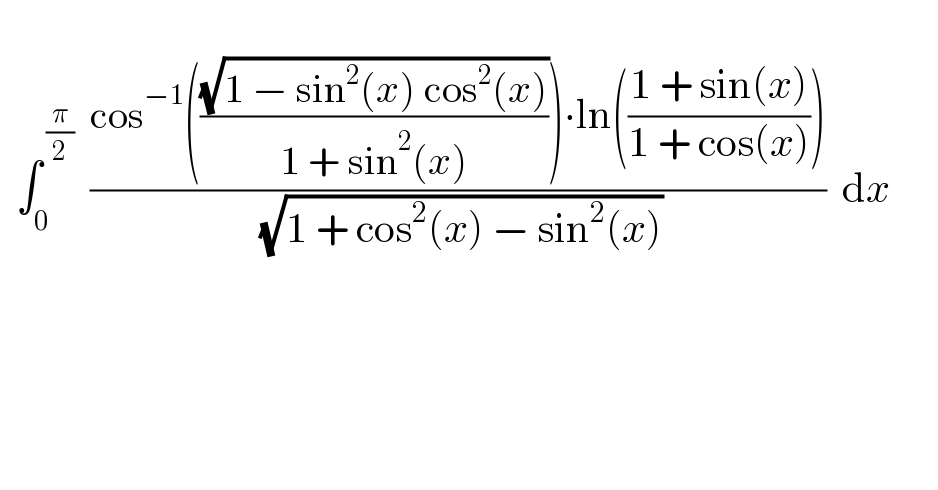
∫_0 ^( (π/2)) ((cos^(−1) (((√(1 − sin^2 (x) cos^2 (x)))/(1 + sin^2 (x))))∙ln(((1 + sin(x))/(1 + cos(x)))))/( (√(1 + cos^2 (x) − sin^2 (x))))) dx

$$ \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{cos}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}\:−\:\mathrm{sin}^{\mathrm{2}} \left({x}\right)\:\mathrm{cos}^{\mathrm{2}} \left({x}\right)}}{\mathrm{1}\:+\:\mathrm{sin}^{\mathrm{2}} \left({x}\right)}\right)\centerdot\mathrm{ln}\left(\frac{\mathrm{1}\:+\:\mathrm{sin}\left({x}\right)}{\mathrm{1}\:+\:\mathrm{cos}\left({x}\right)}\right)}{\:\sqrt{\mathrm{1}\:+\:\mathrm{cos}^{\mathrm{2}} \left({x}\right)\:−\:\mathrm{sin}^{\mathrm{2}} \left({x}\right)}}\:\:\mathrm{d}{x}\:\:\:\:\:\: \\ $$$$ \\ $$

Answered by MathematicalUser2357 last updated on 21/Jun/25

0

$$\mathrm{0} \\ $$

Commented by MathematicalUser2357 last updated on 21/Jun/25

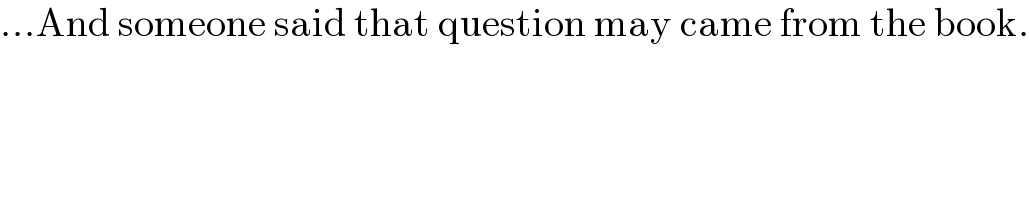
...And someone said that question may came from the book.

$$...\mathrm{And}\:\mathrm{someone}\:\mathrm{said}\:\mathrm{that}\:\mathrm{question}\:\mathrm{may}\:\mathrm{came}\:\mathrm{from}\:\mathrm{the}\:\mathrm{book}. \\ $$

Answered by MrGaster last updated on 21/Jun/25

Terms of Service

Privacy Policy

Contact: info@tinkutara.com