
Question Number 43627 by peter frank last updated on 12/Sep/18
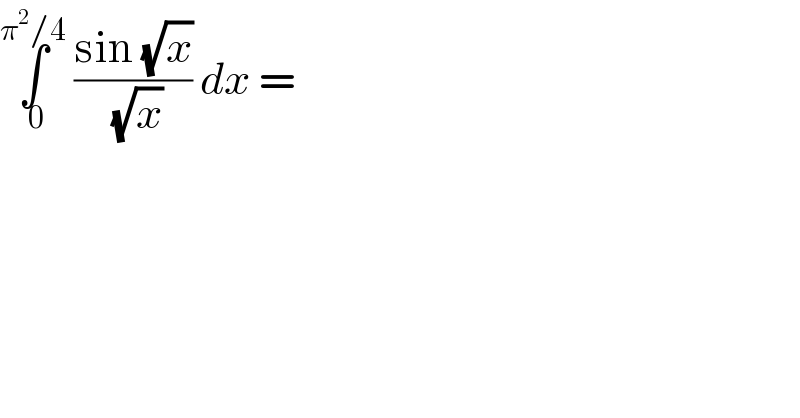
$$\underset{\:\mathrm{0}} {\overset{\pi^{\mathrm{2}} /\mathrm{4}} {\int}}\:\frac{\mathrm{sin}\:\sqrt{{x}}}{\sqrt{{x}}}\:{dx}\:= \\ $$
Commented by math khazana by abdo last updated on 13/Sep/18
![changement (√x)=t give I = ∫_0 ^(π/2) ((sint)/t) (2t)dt = 2 ∫_0 ^(π/2) sin(t)dt =2[−cost]_0 ^(π/2) =2 .](Q43632.png)
$${changement}\:\sqrt{{x}}={t}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sint}}{{t}}\:\left(\mathrm{2}{t}\right){dt}\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left({t}\right){dt} \\ $$$$=\mathrm{2}\left[−{cost}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{2}\:. \\ $$
