
Question Number 136969 by liberty last updated on 28/Mar/21
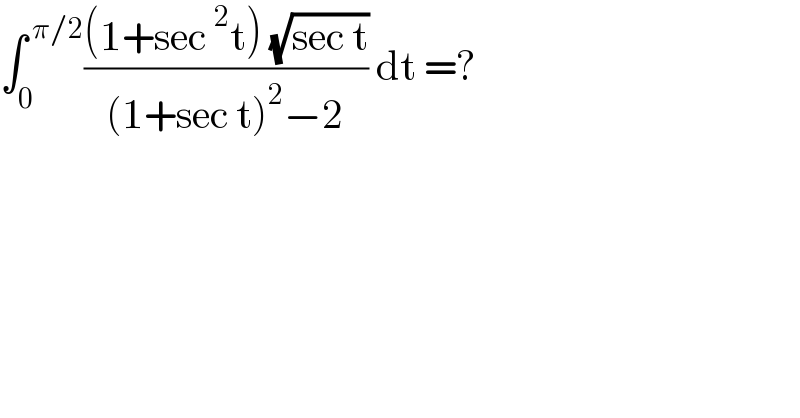
$$\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\left(\mathrm{1}+\mathrm{sec}\:^{\mathrm{2}} \mathrm{t}\right)\:\sqrt{\mathrm{sec}\:\mathrm{t}}}{\left(\mathrm{1}+\mathrm{sec}\:\mathrm{t}\right)^{\mathrm{2}} −\mathrm{2}}\:\mathrm{dt}\:=?\: \\ $$
Answered by EDWIN88 last updated on 28/Mar/21
![E = ∫_0 ^( π/2) (((1+sec^2 t)(√(sec t)))/((1+sec t)^2 −2)) dt E=∫_0 ^( π/2) ((1+cos^2 t)/( (√(cos t)) (1+2cos t−cos^2 t))) dt making change of variable u =(√(cos t)) E=∫_1 ^( 0) ((u^4 +1)/(u(1+2u^2 −u^4 ))).(−((2u)/( (√(1−u^4 )))))du E=2∫_0 ^( 1) ((u^4 +1)/((1+2u^2 −u^4 )(√(1−u^4 )))) du E=2∫_0 ^( 1) ((1+u^(−4) )/((u^(−2) +2−u^2 )(√(u^(−2) −u^2 )))) du set (√(u^(−2) −u^2 )) = v E = 2∫_0 ^( ∞) (dv/(v^2 +2)) = (√2) [arctan ((v/( (√2))))]_0 ^∞ E = (π/( (√2))) .](Q136972.png)
$$\:\mathrm{E}\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\left(\mathrm{1}+\mathrm{sec}^{\mathrm{2}} \:\mathrm{t}\right)\sqrt{\mathrm{sec}\:\mathrm{t}}}{\left(\mathrm{1}+\mathrm{sec}\:\mathrm{t}\right)^{\mathrm{2}} −\mathrm{2}}\:\mathrm{dt} \\ $$$$\mathrm{E}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \frac{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{t}}{\:\sqrt{\mathrm{cos}\:\mathrm{t}}\:\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{t}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{t}\right)}\:\mathrm{dt} \\ $$$$\mathrm{making}\:\mathrm{change}\:\mathrm{of}\:\mathrm{variable}\:\mathrm{u}\:=\sqrt{\mathrm{cos}\:\mathrm{t}} \\ $$$$\mathrm{E}=\int_{\mathrm{1}} ^{\:\mathrm{0}} \:\frac{\mathrm{u}^{\mathrm{4}} +\mathrm{1}}{\mathrm{u}\left(\mathrm{1}+\mathrm{2u}^{\mathrm{2}} −\mathrm{u}^{\mathrm{4}} \right)}.\left(−\frac{\mathrm{2u}}{\:\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{4}} }}\right)\mathrm{du} \\ $$$$\mathrm{E}=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{4}} +\mathrm{1}}{\left(\mathrm{1}+\mathrm{2u}^{\mathrm{2}} −\mathrm{u}^{\mathrm{4}} \right)\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{4}} }}\:\mathrm{du} \\ $$$$\mathrm{E}=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}+\mathrm{u}^{−\mathrm{4}} }{\left(\mathrm{u}^{−\mathrm{2}} +\mathrm{2}−\mathrm{u}^{\mathrm{2}} \right)\sqrt{\mathrm{u}^{−\mathrm{2}} −\mathrm{u}^{\mathrm{2}} }}\:\mathrm{du} \\ $$$$\mathrm{set}\:\sqrt{\mathrm{u}^{−\mathrm{2}} −\mathrm{u}^{\mathrm{2}} }\:=\:\mathrm{v}\: \\ $$$$\mathrm{E}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} +\mathrm{2}}\:=\:\sqrt{\mathrm{2}}\:\left[\mathrm{arctan}\:\left(\frac{\mathrm{v}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{E}\:=\:\frac{\pi}{\:\sqrt{\mathrm{2}}}\:. \\ $$
Commented by liberty last updated on 28/Mar/21

$$\mathrm{great} \\ $$
