Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 145385 by mnjuly1970 last updated on 04/Jul/21

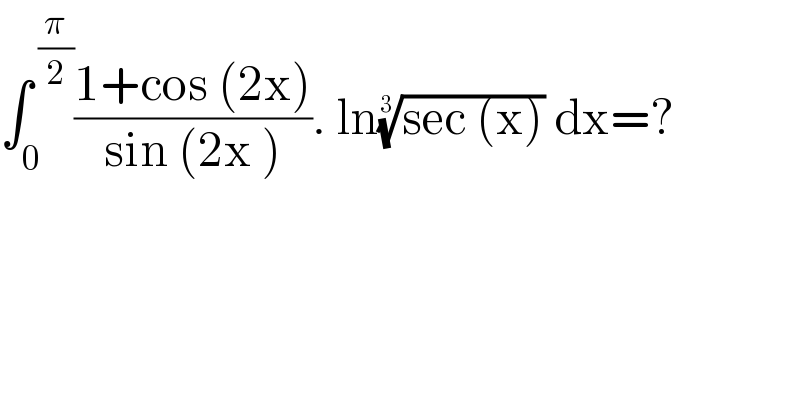
∫_0 ^( (π/2)) ((1+cos (2x))/(sin (2x ))). ln((sec (x)))^(1/3) dx=?

$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{cos}\:\left(\mathrm{2x}\right)}{\mathrm{sin}\:\left(\mathrm{2x}\:\right)}.\:\mathrm{ln}\sqrt[{\mathrm{3}}]{\mathrm{sec}\:\left(\mathrm{x}\right)}\:\mathrm{dx}=? \\ $$

Answered by mindispower last updated on 04/Jul/21

cos(2x)=2cos^2 (x)−1 ⇔−(1/3)∫_0 ^(π/2) ((cos(x))/(sin(x)))ln(cos(x))dx =−(1/(12)).∂_a 2∫_0 ^(π/2) cos^(2a−1) (x)sin^(2b−1) (x)dx∣_((a,b)=((3/2),0)) =−lim_(b→0) (1/(12))∂_a β(a,b)∣(a,b)=((3/2),b) =−lim_(b→0) (1/(12))β(a,b)(Ψ(a)−Ψ(a+b)) =−(1/(12)) lim_(b→0) Γ(b)(Ψ((3/2))−Ψ((3/2)+b) =−(1/(12))(Ψ((3/2))−Ψ((3/2)+b))Γ(b) Ψ(a)−Ψ(a+h)=−Ψ′(a)h Ψ((3/2))−Ψ((3/2)+b)=−Ψ′((3/2))b ⇔(1/(12))lim_(b→0) bΓ(b)Ψ′((3/2))=(1/(12))Γ(1+b)Ψ′((3/2))=((Ψ′((3/2)))/(12))

$${cos}\left(\mathrm{2}{x}\right)=\mathrm{2}{cos}^{\mathrm{2}} \left({x}\right)−\mathrm{1} \\ $$$$\Leftrightarrow−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}\left({x}\right)}{{sin}\left({x}\right)}{ln}\left({cos}\left({x}\right)\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}.\partial_{{a}} \mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{a}−\mathrm{1}} \left({x}\right){sin}^{\mathrm{2}{b}−\mathrm{1}} \left({x}\right){dx}\mid_{\left({a},{b}\right)=\left(\frac{\mathrm{3}}{\mathrm{2}},\mathrm{0}\right)} \\ $$$$=−\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{12}}\partial_{{a}} \beta\left({a},{b}\right)\mid\left({a},{b}\right)=\left(\frac{\mathrm{3}}{\mathrm{2}},{b}\right) \\ $$$$=−\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{12}}\beta\left({a},{b}\right)\left(\Psi\left({a}\right)−\Psi\left({a}+{b}\right)\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}\:\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\Gamma\left({b}\right)\left(\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}+{b}\right)\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}\left(\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}+{b}\right)\right)\Gamma\left({b}\right) \\ $$$$\Psi\left({a}\right)−\Psi\left({a}+{h}\right)=−\Psi'\left({a}\right){h} \\ $$$$\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}+{b}\right)=−\Psi'\left(\frac{\mathrm{3}}{\mathrm{2}}\right){b} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{12}}\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}{b}\Gamma\left({b}\right)\Psi'\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{12}}\Gamma\left(\mathrm{1}+{b}\right)\Psi'\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\Psi'\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{12}} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 04/Jul/21

thank you so much..

$${thank}\:{you}\:{so}\:{much}.. \\ $$

Commented by mindispower last updated on 04/Jul/21

pleasur sir

$${pleasur}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com