
Question Number 65760 by mmkkmm000m last updated on 03/Aug/19
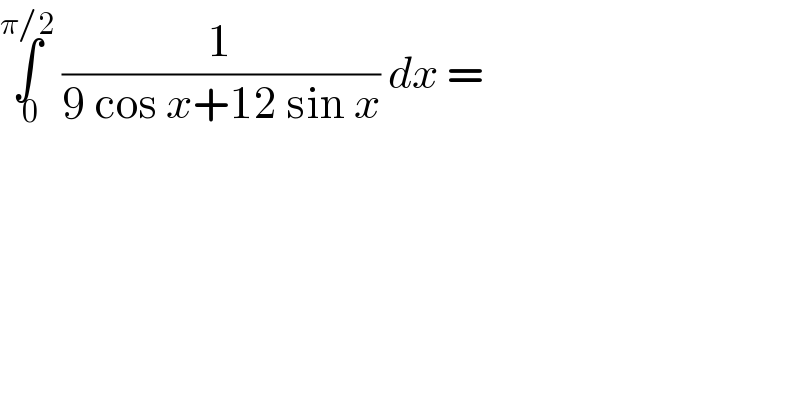
$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{1}}{\mathrm{9}\:\mathrm{cos}\:{x}+\mathrm{12}\:\mathrm{sin}\:{x}}\:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 04/Aug/19
![let I =∫_0 ^(π/2) (dx/(9cosx +12sinx)) ⇒3I =∫_0 ^(π/2) (dx/(3cosx+4sinx)) =_(tan((x/2))=t) ∫_0 ^1 (1/(3((1−t^2 )/(1+t^2 )) +4((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^1 ((2dt)/(3−3t^2 +8t)) =∫_0 ^1 ((−2dt)/(3t^2 −8t −3)) 3t^2 −8t −3 =0 →Δ^′ =16+9 =25 ⇒t_1 =((4+5)/3) =3 and t_2 =((4−5)/3) =−(1/3) ⇒((−2)/(3t^2 −8t −3)) =((−2)/(3(t−3)(t+(1/3)))) =−(2/3)×(3/8){(1/(t−3))−(1/(t+(1/3)))} =−(1/4){(1/(t−3))−(1/(t+(1/3)))} ⇒ ∫_0 ^1 ((−2dt)/(3t^2 −8t −3)) =−(1/4)[ln∣((t−3)/(t+(1/3)))∣]_0 ^1 =−(1/4){ln((2/(4/3)))−ln(9)} =−(1/4){ln((3/2))−2ln(3)} =−(1/4){−ln(3)−ln(2)} =((ln(6))/4) ⇒ I =((ln(6))/(12))](Q65793.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{9}{cosx}\:+\mathrm{12}{sinx}}\:\Rightarrow\mathrm{3}{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{3}{cosx}+\mathrm{4}{sinx}} \\ $$$$=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{3}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{4}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{\mathrm{3}−\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{8}{t}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{2}{dt}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}\:−\mathrm{3}} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}\:−\mathrm{3}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{16}+\mathrm{9}\:=\mathrm{25}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{4}+\mathrm{5}}{\mathrm{3}}\:=\mathrm{3}\:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{4}−\mathrm{5}}{\mathrm{3}}\:=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{−\mathrm{2}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}\:−\mathrm{3}}\:=\frac{−\mathrm{2}}{\mathrm{3}\left({t}−\mathrm{3}\right)\left({t}+\frac{\mathrm{1}}{\mathrm{3}}\right)}\:=−\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{8}}\left\{\frac{\mathrm{1}}{{t}−\mathrm{3}}−\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{\mathrm{3}}}\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{\mathrm{1}}{{t}−\mathrm{3}}−\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{\mathrm{3}}}\right\}\:\Rightarrow \\ $$$$\overset{\mathrm{1}} {\int}_{\mathrm{0}} \:\frac{−\mathrm{2}{dt}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}\:−\mathrm{3}}\:=−\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\mid\frac{{t}−\mathrm{3}}{{t}+\frac{\mathrm{1}}{\mathrm{3}}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{4}}\left\{{ln}\left(\frac{\mathrm{2}}{\frac{\mathrm{4}}{\mathrm{3}}}\right)−{ln}\left(\mathrm{9}\right)\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\left\{{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{2}{ln}\left(\mathrm{3}\right)\right\}\:=−\frac{\mathrm{1}}{\mathrm{4}}\left\{−{ln}\left(\mathrm{3}\right)−{ln}\left(\mathrm{2}\right)\right\}\:=\frac{{ln}\left(\mathrm{6}\right)}{\mathrm{4}}\:\Rightarrow \\ $$$${I}\:=\frac{{ln}\left(\mathrm{6}\right)}{\mathrm{12}} \\ $$
Commented by mathmax by abdo last updated on 04/Aug/19
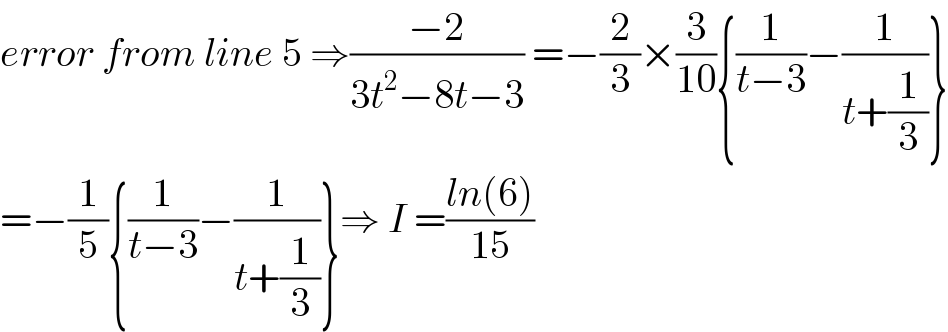
$${error}\:{from}\:{line}\:\mathrm{5}\:\Rightarrow\frac{−\mathrm{2}}{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}−\mathrm{3}}\:=−\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{10}}\left\{\frac{\mathrm{1}}{{t}−\mathrm{3}}−\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{\mathrm{3}}}\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}\left\{\frac{\mathrm{1}}{{t}−\mathrm{3}}−\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{\mathrm{3}}}\right\}\Rightarrow\:{I}\:=\frac{{ln}\left(\mathrm{6}\right)}{\mathrm{15}} \\ $$
Answered by Tanmay chaudhury last updated on 03/Aug/19
![or method ∫_0 ^(π/2) (dx/(15((9/(15))cosx+((12)/(15))sinx))) (1/(15))∫_0 ^(π/2) cosec(x+α)dx [(9/(15))=sinα ((12)/(15))=cosα] (1/(15))∣lntan(((x+α)/2))∣_0 ^(π/2) (1/(15))lntan[(π/4)+(1/2)tan^(−1) ((9/(12)))]−(1/(15))lntan[(1/2)tan^(−1) ((9/(12)))]](Q65780.png)
$${or}\:{method} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{15}\left(\frac{\mathrm{9}}{\mathrm{15}}{cosx}+\frac{\mathrm{12}}{\mathrm{15}}{sinx}\right)}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{15}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cosec}\left({x}+\alpha\right){dx}\:\:\:\:\left[\frac{\mathrm{9}}{\mathrm{15}}={sin}\alpha\:\:\:\frac{\mathrm{12}}{\mathrm{15}}={cos}\alpha\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{15}}\mid{lntan}\left(\frac{{x}+\alpha}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{15}}{lntan}\left[\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{12}}\right)\right]−\frac{\mathrm{1}}{\mathrm{15}}{lntan}\left[\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{12}}\right)\right] \\ $$
